
Question Number 64871 by Rio Michael last updated on 22/Jul/19

$${any}\:{hint}\:{about}\:{how}\:{to}\:{prove}\:{by}\:{induction}\:{in}\:{the}\:{Sigma}\:{notion}\:{topic}? \\ $$$${like}\:{in}\:\Sigma \\ $$
Commented by mathmax by abdo last updated on 22/Jul/19

$${you}\:{question}\:{is}\:{not}\:{clear}.... \\ $$
Commented by Rio Michael last updated on 22/Jul/19
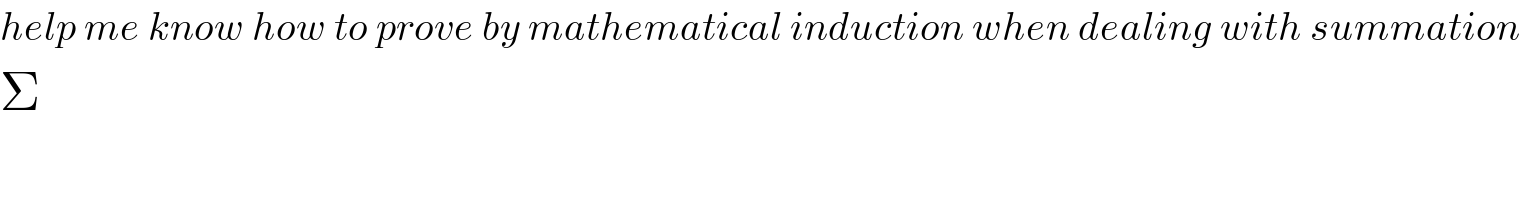
$${help}\:{me}\:{know}\:{how}\:{to}\:{prove}\:{by}\:{mathematical}\:{induction}\:{when}\:{dealing}\:{with}\:{summation} \\ $$$$\Sigma \\ $$
Commented by mathmax by abdo last updated on 22/Jul/19
![i dont understand what you want but i give some properties of of Σ if we have (x_i ) _(1≤i≤n) and (y_i )_(i∈[0,n]) 2 sequences of reals numbers (or complex) the sum x_1 +x_2 +....+x_k is writen Σ_(i=1) ^k x_i also we have Σ_(i=1) ^n x_i +^− Σ_(i=1) ^n y_i =Σ_(i=1) ^n (x_i +^− y_i ) Σ_(i=1) ^n λ x_i =λ Σ_(i=1) ^n x_i (λ ∈R or C) Σ_(i=1) ^n (1) =n ,Σ_(i=0) ^n (1) =n+1 ,Σ_(i=1) ^n λ =nλ Σ_(i=0) ^n λ =(n+1)λ , Σ_i Σ_j x_(ij) =Σ_j Σ_i x_(ij) ....](Q64889.png)
$${i}\:{dont}\:{understand}\:{what}\:{you}\:{want}\:{but}\:{i}\:{give}\:{some}\:{properties}\:{of} \\ $$$${of}\:\:\Sigma\:\:\:\:{if}\:{we}\:{have}\:\:\left({x}_{{i}} \right)\:_{\mathrm{1}\leqslant{i}\leqslant{n}} \:\:{and}\:\left({y}_{{i}} \right)_{{i}\in\left[\mathrm{0},{n}\right]} \:\mathrm{2}\:{sequences}\:{of}\:{reals} \\ $$$${numbers}\:\left({or}\:{complex}\right)\:\:{the}\:{sum}\:{x}_{\mathrm{1}} \:+{x}_{\mathrm{2}} +....+{x}_{{k}} \:{is}\:{writen} \\ $$$$\sum_{{i}=\mathrm{1}} ^{{k}} \:{x}_{{i}} \:\:\:\:{also}\:{we}\:{have}\:\sum_{{i}=\mathrm{1}} ^{{n}} \:{x}_{{i}} \:\overset{−} {+}\sum_{{i}=\mathrm{1}} ^{{n}} \:{y}_{{i}} =\sum_{{i}=\mathrm{1}} ^{{n}} \left({x}_{{i}} \:\overset{−} {+}{y}_{{i}} \right) \\ $$$$\sum_{{i}=\mathrm{1}} ^{{n}} \:\lambda\:{x}_{{i}} =\lambda\:\sum_{{i}=\mathrm{1}} ^{{n}} \:{x}_{{i}} \:\:\left(\lambda\:\in{R}\:{or}\:{C}\right) \\ $$$$\sum_{{i}=\mathrm{1}} ^{{n}} \left(\mathrm{1}\right)\:={n}\:\:\:,\sum_{{i}=\mathrm{0}} ^{{n}} \left(\mathrm{1}\right)\:={n}+\mathrm{1}\:,\sum_{{i}=\mathrm{1}} ^{{n}} \lambda\:={n}\lambda \\ $$$$\sum_{{i}=\mathrm{0}} ^{{n}} \:\lambda\:=\left({n}+\mathrm{1}\right)\lambda\:\:\:\:,\:\sum_{{i}} \:\sum_{{j}} \:{x}_{{ij}} =\sum_{{j}} \sum_{{i}} {x}_{{ij}} \:\:.... \\ $$$$ \\ $$
Commented by Rio Michael last updated on 22/Jul/19
$${well}\:{thanks}\:{for}\:{that} \\ $$
Commented by mathmax by abdo last updated on 23/Jul/19
$${you}\:{are}\:{welcome}. \\ $$
