
Question Number 64778 by aliesam last updated on 21/Jul/19
Commented by som(math1967) last updated on 21/Jul/19
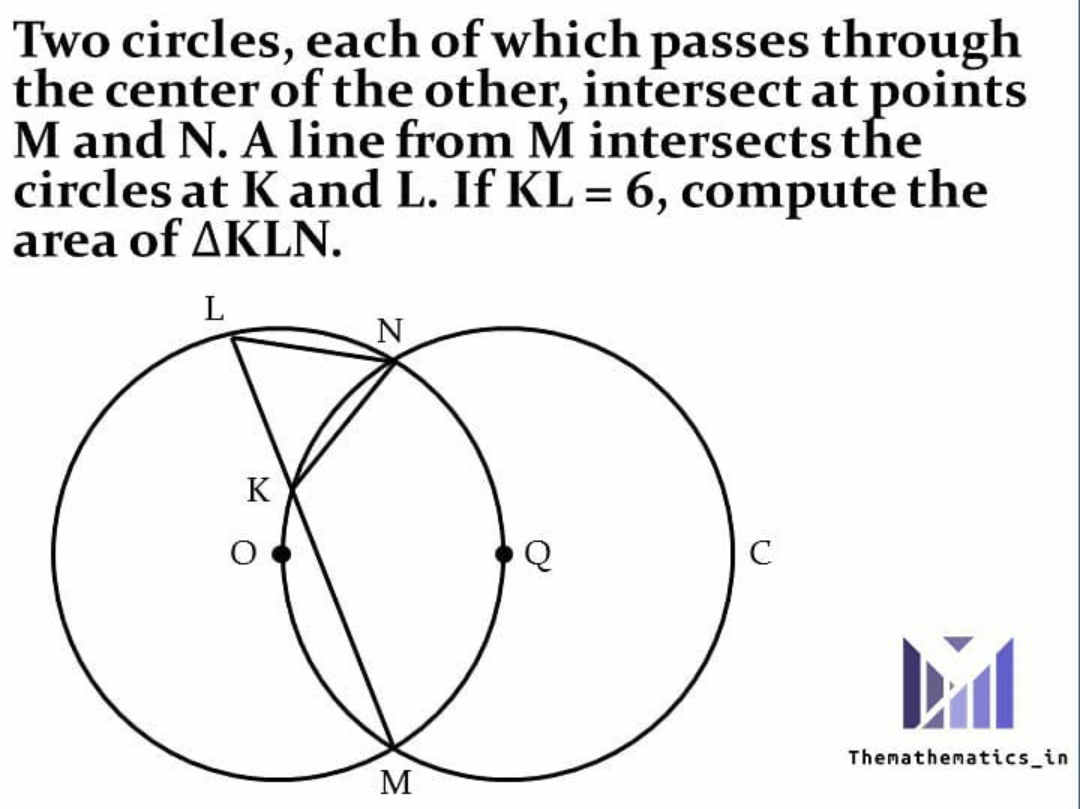
![join O,Q O,N O,M M,Q N,Q now ON=NQ=OQ=OM=MQ ∴∠NOM=60+60=120° ∠MLN=(1/2)∠NOM=60° ∠NKM=∠NOM=120° [subtend on same segment] now ext∠NKM=∠NLK+∠LNK ∴∠LNK=120−60=60 so △KLN equilateral](Q64782.png)
$${join}\:{O},{Q}\:\:{O},{N}\:{O},{M}\:\:{M},{Q}\:{N},{Q} \\ $$$${now}\:{ON}={NQ}={OQ}={OM}={MQ} \\ $$$$\therefore\angle{NOM}=\mathrm{60}+\mathrm{60}=\mathrm{120}° \\ $$$$\angle{MLN}=\frac{\mathrm{1}}{\mathrm{2}}\angle{NOM}=\mathrm{60}° \\ $$$$\angle{NKM}=\angle{NOM}=\mathrm{120}°\:\:\left[{subtend}\:{on}\:{same}\:{segment}\right] \\ $$$${now}\:{ext}\angle{NKM}=\angle{NLK}+\angle{LNK} \\ $$$$\therefore\angle{LNK}=\mathrm{120}−\mathrm{60}=\mathrm{60} \\ $$$${so}\:\bigtriangleup{KLN}\:{equilateral} \\ $$
Commented by aliesam last updated on 21/Jul/19

$${god}\:{bless}\:{you} \\ $$
Answered by som(math1967) last updated on 21/Jul/19
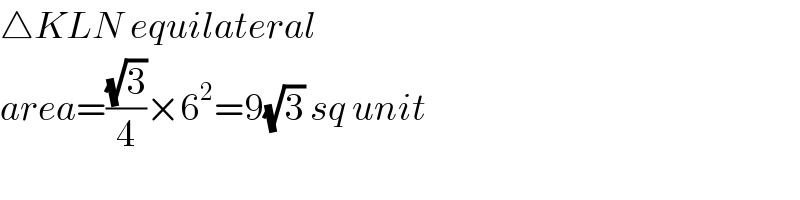
$$\bigtriangleup{KLN}\:{equilateral} \\ $$$${area}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}×\mathrm{6}^{\mathrm{2}} =\mathrm{9}\sqrt{\mathrm{3}}\:{sq}\:{unit} \\ $$
