
Question Number 64773 by ankan0 last updated on 21/Jul/19
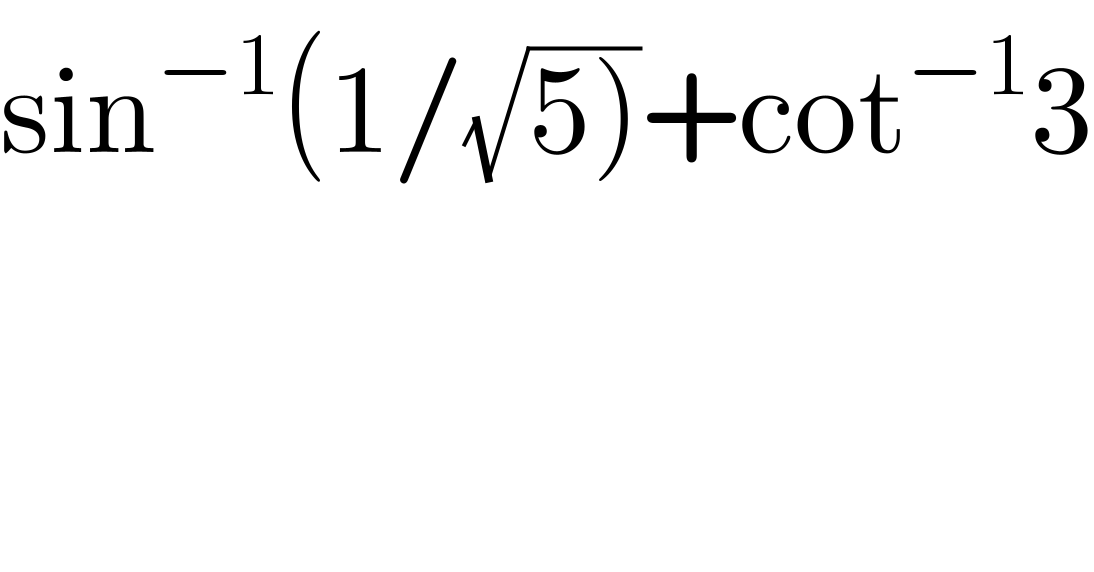
$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}/\sqrt{\left.\mathrm{5}\right)}+\mathrm{cot}^{−\mathrm{1}} \mathrm{3}\right. \\ $$
Answered by Kunal12588 last updated on 21/Jul/19
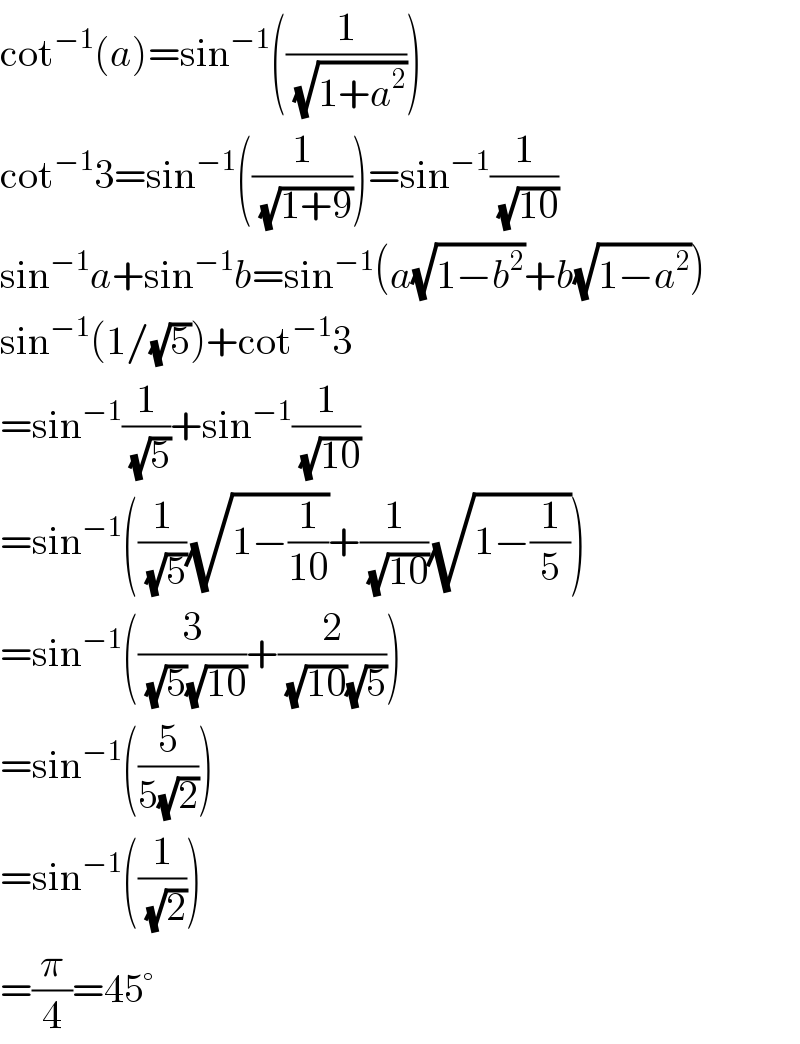
$$\mathrm{cot}^{−\mathrm{1}} \left({a}\right)=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{a}^{\mathrm{2}} }}\right) \\ $$$$\mathrm{cot}^{−\mathrm{1}} \mathrm{3}=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{1}+\mathrm{9}}}\right)=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\sqrt{\mathrm{10}}} \\ $$$$\mathrm{sin}^{−\mathrm{1}} {a}+\mathrm{sin}^{−\mathrm{1}} {b}=\mathrm{sin}^{−\mathrm{1}} \left({a}\sqrt{\mathrm{1}−{b}^{\mathrm{2}} }+{b}\sqrt{\mathrm{1}−{a}^{\mathrm{2}} }\right) \\ $$$$\mathrm{sin}^{−\mathrm{1}} \left(\mathrm{1}/\sqrt{\mathrm{5}}\right)+\mathrm{cot}^{−\mathrm{1}} \mathrm{3} \\ $$$$=\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\sqrt{\mathrm{5}}}+\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{1}}{\sqrt{\mathrm{10}}} \\ $$$$=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{5}}}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}}+\frac{\mathrm{1}}{\sqrt{\mathrm{10}}}\sqrt{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{5}}}\right) \\ $$$$=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{3}}{\sqrt{\mathrm{5}}\sqrt{\mathrm{10}}}+\frac{\mathrm{2}}{\sqrt{\mathrm{10}}\sqrt{\mathrm{5}}}\right) \\ $$$$=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{5}}{\mathrm{5}\sqrt{\mathrm{2}}}\right) \\ $$$$=\mathrm{sin}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\right) \\ $$$$=\frac{\pi}{\mathrm{4}}=\mathrm{45}° \\ $$
Commented by John M. Kaloki last updated on 13/Aug/19

$${I}\:{can} \\ $$
