
Question Number 64625 by ajfour last updated on 19/Jul/19
Commented by ajfour last updated on 19/Jul/19

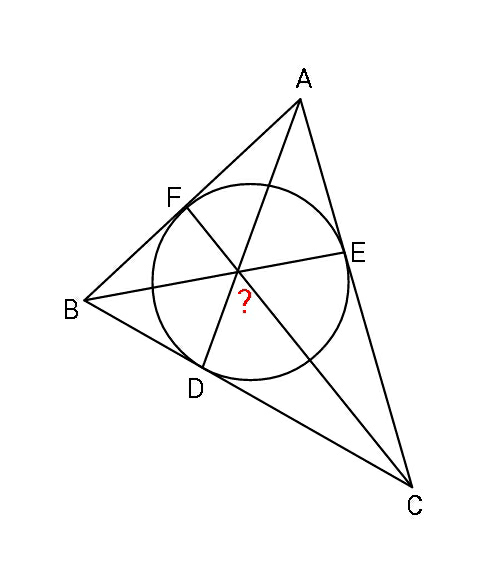
$${Are}\:{AD},\:{BE},\:{CF}\:\:{concurrent} \\ $$$${generally}?\:{please}\:{help}\:{check}. \\ $$
Commented by MJS last updated on 20/Jul/19

$$\mathrm{yes} \\ $$$$\mathrm{I}\:\mathrm{will}\:\mathrm{show}\:\mathrm{it}\:\mathrm{tomorrow} \\ $$
Commented by MJS last updated on 20/Jul/19

$$\mid{AE}\mid=\mid{AF}\mid \\ $$$$\mid{BF}\mid=\mid{BD}\mid \\ $$$$\mid{CD}\mid=\mid{CE}\mid \\ $$$$\mathrm{is}\:\mathrm{it}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{show}\:\mathrm{geometrically}?\:\mathrm{it}\:\mathrm{reminds} \\ $$$$\mathrm{of}\:\mathrm{Heron}'\mathrm{s}\:\mathrm{method}... \\ $$$$\mathrm{I}\:\mathrm{can}\:``\mathrm{only}''\:\mathrm{calculate}\:\mathrm{it} \\ $$
Answered by ajfour last updated on 20/Jul/19
Commented by ajfour last updated on 20/Jul/19
![BC=a, CA=b, AB=c (vector) ⇒ a+b+c=0 ((BD)/(DC))=p , ((CE)/(EA))=q , ((AF)/(FB))=r eq. of BE r=λ(a+qb) eq. of CF r=a+μ(1−r)c eq. of AD r=pa+ρ(−c−ap) Intersection of BE & CF OG_1 =λ(a+qb)=a+μ(1−r)c ⇒ λ(a+qb)=a−μ(1−r)(a+b) ⇒ λ=1−μ(1−r) ...(i) λq=−μ(1−r) ...(ii) Similarly from intersection of CF & AD , OG_2 = a−μ(1−r)(a+b)=pa+ρ(a+b−ap) ⇒ 1−μ(1−r)=p+ρ(1−p) ...(iii) −μ(1−r)=ρ ...(iv) Also ∣a∣p=∣c∣(1−r) ∣b∣q=∣a∣(1−p) ∣c∣r=∣b∣(1−q) And since ∣a∣p+∣b∣q=∣a∣ ∣b∣q+∣c∣r=∣b∣ ∣c∣r+∣a∣p=∣c∣ if we let ∣s∣=∣a∣+∣b∣+∣c∣ ⇒ ∣a∣p=∣s∣−∣b∣ , ∣b∣q=∣s∣−∣c∣, ∣c∣r=∣s∣−∣a∣ Now from (i)&(ii) 1−λ=μ(1−r) λq=μ(r−1) ⇒ λ−1=λq ⇒ λ=(1/(1−q))=(1/(1−((∣s∣−∣c∣)/(∣b∣))))=((∣b∣)/(∣b∣+∣c∣−∣s∣)) μ=((1−λ)/(1−r))=(((((∣c∣−∣s∣)/(∣b∣+∣c∣−∣s∣))))/(1−((∣s∣−∣a∣)/(∣c∣)))) ⇒ μ=((∣c∣(∣c∣−∣s∣))/((∣b∣+∣c∣−∣s∣)(∣c∣+∣a∣−∣s∣))) OG_1 =λ(a+qb)=a+μ(1−r)c =((∣b∣)/(∣b∣+∣c∣−∣s∣))[a+(((∣s∣−∣c∣)/(∣b∣)))b] OG_2 =a−μ(1−r)(a+b) =a−((∣c∣(∣c∣−∣s∣)(1−((∣s∣−∣a∣)/(∣c∣)))(a+b))/((∣b∣+∣c∣−∣s∣)(∣c∣+∣a∣−∣s∣))) =a−(((∣c∣−∣s∣)(a+b))/(∣b∣+∣c∣−∣s∣)) OG_2 =((∣b∣)/(∣b∣+∣c∣−∣s∣))[a+(((∣s∣−∣c∣)/(∣b∣)))b] ⇒ OG_2 =OG_1 hence AD, BE, CF are concurrent.](Q64679.png)
$${BC}={a},\:{CA}={b},\:{AB}={c}\:\:\:\left({vector}\right) \\ $$$$\Rightarrow\:\:{a}+{b}+{c}=\mathrm{0} \\ $$$$\frac{{BD}}{{DC}}={p}\:,\:\frac{{CE}}{{EA}}={q}\:,\:\frac{{AF}}{{FB}}={r} \\ $$$${eq}.\:{of}\:{BE}\:\:\:\:\:\:\:\:{r}=\lambda\left({a}+{qb}\right) \\ $$$${eq}.\:{of}\:{CF}\:\:\:\:\:\:\:{r}={a}+\mu\left(\mathrm{1}−{r}\right){c} \\ $$$${eq}.\:{of}\:{AD}\:\:\:\:\:\:{r}={pa}+\rho\left(−{c}−{ap}\right) \\ $$$${Intersection}\:{of}\:{BE}\:\&\:{CF} \\ $$$${OG}_{\mathrm{1}} =\lambda\left({a}+{qb}\right)={a}+\mu\left(\mathrm{1}−{r}\right){c} \\ $$$$\Rightarrow\:\:\:\lambda\left({a}+{qb}\right)={a}−\mu\left(\mathrm{1}−{r}\right)\left({a}+{b}\right) \\ $$$$\Rightarrow\:\:\lambda=\mathrm{1}−\mu\left(\mathrm{1}−{r}\right)\:\:\:\:\:\:\:\:\:...\left({i}\right) \\ $$$$\:\:\:\:\:\:\:\lambda{q}=−\mu\left(\mathrm{1}−{r}\right)\:\:\:\:\:\:\:\:\:...\left({ii}\right) \\ $$$${Similarly}\:{from}\:{intersection}\:{of} \\ $$$${CF}\:\&\:{AD}\:,\:\:{OG}_{\mathrm{2}} = \\ $$$$\:\:{a}−\mu\left(\mathrm{1}−{r}\right)\left({a}+{b}\right)={pa}+\rho\left({a}+{b}−{ap}\right) \\ $$$$\Rightarrow\:\:\mathrm{1}−\mu\left(\mathrm{1}−{r}\right)={p}+\rho\left(\mathrm{1}−{p}\right)\:\:\:...\left({iii}\right) \\ $$$$\:\:\:\:\:\:\:\:−\mu\left(\mathrm{1}−{r}\right)=\rho\:\:\:\:\:\:\:\:\:\:\:\:...\left({iv}\right) \\ $$$${Also}\:\:\:\mid{a}\mid{p}=\mid{c}\mid\left(\mathrm{1}−{r}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid{b}\mid{q}=\mid{a}\mid\left(\mathrm{1}−{p}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mid{c}\mid{r}=\mid{b}\mid\left(\mathrm{1}−{q}\right) \\ $$$${And}\:{since}\:\: \\ $$$$\:\:\:\:\:\:\:\:\mid{a}\mid{p}+\mid{b}\mid{q}=\mid{a}\mid \\ $$$$\:\:\:\:\:\:\:\:\mid{b}\mid{q}+\mid{c}\mid{r}=\mid{b}\mid \\ $$$$\:\:\:\:\:\:\:\:\mid{c}\mid{r}+\mid{a}\mid{p}=\mid{c}\mid \\ $$$${if}\:{we}\:{let}\:\:\mid{s}\mid=\mid{a}\mid+\mid{b}\mid+\mid{c}\mid \\ $$$$\Rightarrow\:\mid{a}\mid{p}=\mid{s}\mid−\mid{b}\mid\:,\:\mid{b}\mid{q}=\mid{s}\mid−\mid{c}\mid,\:\mid{c}\mid{r}=\mid{s}\mid−\mid{a}\mid \\ $$$$\mathcal{N}{ow}\:{from}\:\left({i}\right)\&\left({ii}\right) \\ $$$$\:\:\mathrm{1}−\lambda=\mu\left(\mathrm{1}−{r}\right) \\ $$$$\:\:\:\:\:\:\lambda{q}=\mu\left({r}−\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\lambda−\mathrm{1}=\lambda{q} \\ $$$$\Rightarrow\:\:\lambda=\frac{\mathrm{1}}{\mathrm{1}−{q}}=\frac{\mathrm{1}}{\mathrm{1}−\frac{\mid{s}\mid−\mid{c}\mid}{\mid{b}\mid}}=\frac{\mid{b}\mid}{\mid{b}\mid+\mid{c}\mid−\mid{s}\mid} \\ $$$$\:\:\:\:\:\mu=\frac{\mathrm{1}−\lambda}{\mathrm{1}−{r}}=\frac{\left(\frac{\mid{c}\mid−\mid{s}\mid}{\mid{b}\mid+\mid{c}\mid−\mid{s}\mid}\right)}{\mathrm{1}−\frac{\mid{s}\mid−\mid{a}\mid}{\mid{c}\mid}} \\ $$$$\Rightarrow\:\mu=\frac{\mid{c}\mid\left(\mid{c}\mid−\mid{s}\mid\right)}{\left(\mid{b}\mid+\mid{c}\mid−\mid{s}\mid\right)\left(\mid{c}\mid+\mid{a}\mid−\mid{s}\mid\right)} \\ $$$${OG}_{\mathrm{1}} =\lambda\left({a}+{qb}\right)={a}+\mu\left(\mathrm{1}−{r}\right){c} \\ $$$$\:\:\:=\frac{\mid{b}\mid}{\mid{b}\mid+\mid{c}\mid−\mid{s}\mid}\left[{a}+\left(\frac{\mid{s}\mid−\mid{c}\mid}{\mid{b}\mid}\right){b}\right] \\ $$$${OG}_{\mathrm{2}} ={a}−\mu\left(\mathrm{1}−{r}\right)\left({a}+{b}\right) \\ $$$$\:\:\:\:\:\:\:={a}−\frac{\mid{c}\mid\left(\mid{c}\mid−\mid{s}\mid\right)\left(\mathrm{1}−\frac{\mid{s}\mid−\mid{a}\mid}{\mid{c}\mid}\right)\left({a}+{b}\right)}{\left(\mid{b}\mid+\mid{c}\mid−\mid{s}\mid\right)\left(\mid{c}\mid+\mid{a}\mid−\mid{s}\mid\right)} \\ $$$$\:\:\:\:={a}−\frac{\left(\mid{c}\mid−\mid{s}\mid\right)\left({a}+{b}\right)}{\mid{b}\mid+\mid{c}\mid−\mid{s}\mid} \\ $$$${OG}_{\mathrm{2}} =\frac{\mid{b}\mid}{\mid{b}\mid+\mid{c}\mid−\mid{s}\mid}\left[{a}+\left(\frac{\mid{s}\mid−\mid{c}\mid}{\mid{b}\mid}\right){b}\right] \\ $$$$\Rightarrow\:\:\:{OG}_{\mathrm{2}} ={OG}_{\mathrm{1}} \\ $$$${hence}\:{AD},\:{BE},\:{CF}\:\:{are}\:{concurrent}. \\ $$
Commented by MJS last updated on 20/Jul/19

$$\mathrm{great}!\:\mathrm{as}\:\mathrm{I}\:\mathrm{mentioned}\:\mathrm{before},\:\mathrm{your}\:\mathrm{thinking} \\ $$$$\mathrm{is}\:\mathrm{very}\:\mathrm{different}\:\mathrm{from}\:\mathrm{mine},\:\mathrm{always}\:\mathrm{interesting} \\ $$$$\mathrm{to}\:\mathrm{follow}\:\mathrm{your}\:\mathrm{paths}\:\mathrm{to}\:\mathrm{the}\:\mathrm{same}\:\mathrm{results} \\ $$
Commented by mr W last updated on 20/Jul/19

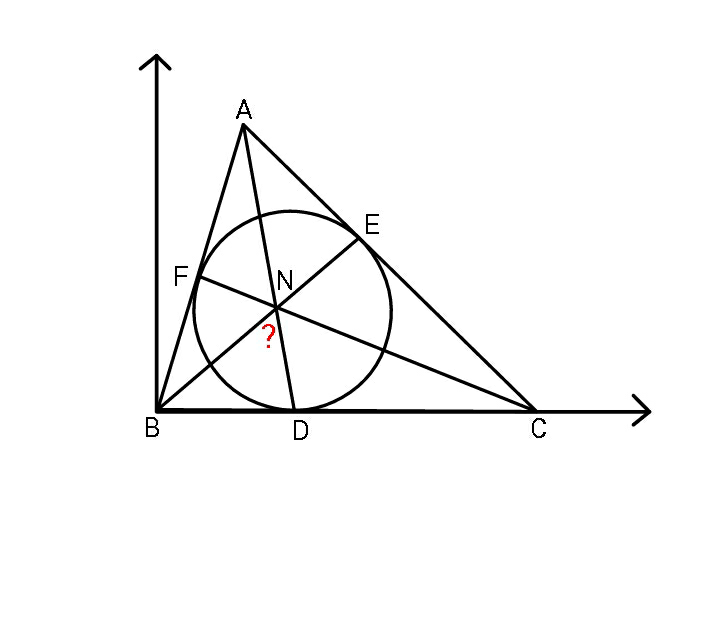
$${nice}\:{proof}\:{sir}!\:{this}\:{is}\:{what}\:{i}\:{prefered} \\ $$$${and}\:{expected}. \\ $$$${i}\:{knew}\:{you}\:{would}\:{change}\:{to}\:{the}\:{vector}\: \\ $$$${method}\:{as}\:{i}\:{saw}\:{your}\:{previous}\:{post}\:{sir}. \\ $$$${i}\:{started}\:{last}\:{evening}\:{before}\:{going}\:{sleep} \\ $$$${also}\:{with}\:{similar}\:{vector}\:{method},\:{trying} \\ $$$${to}\:{use}\:{perp}\:{dot}\:{product},\:{but}\:{today}\:{i}\:{had} \\ $$$${no}\:{time}\:{to}\:{finish}\:{it}.\:{besides}\:{i}'{m}\:{not} \\ $$$${such}\:{familiar}\:{with}\:{vector}\:{operations} \\ $$$${and}\:{so}\:\:{i}'{ll}\:{need}\:{some}\:{more}\:{time}.\:{now} \\ $$$${i}\:{can}\:{study}\:{your}\:{solution}\:{and}\:{learn}\: \\ $$$${from}\:{it}. \\ $$$${because}\:{it}'{s}\:{so}\:{interesting}\:{to}\:{see}\:{that}\: \\ $$$${we}\:{had}\:{very}\:{similar}\:{thoughts}\:{and} \\ $$$${use}\:{even}\:{some}\:{identical}\:{symbols},\:{i}'{m} \\ $$$${showing}\:{you}\:{a}\:{page}\:{of}\:{my}\:{trying} \\ $$$${last}\:{evening}. \\ $$
Commented by mr W last updated on 20/Jul/19

Commented by ajfour last updated on 20/Jul/19
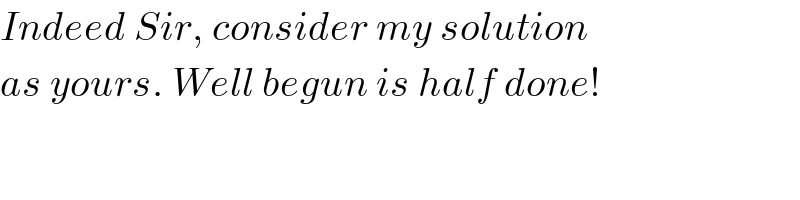
$${Indeed}\:{Sir},\:{consider}\:{my}\:{solution} \\ $$$${as}\:{yours}.\:{Well}\:{begun}\:{is}\:{half}\:{done}! \\ $$
Commented by mr W last updated on 20/Jul/19

$${thank}\:{you}\:{sir}!\:{concerning}\:{vector} \\ $$$${method}\:{i}\:{want}\:{to}\:{learn}\:{from}\:{you}. \\ $$
Answered by MJS last updated on 20/Jul/19

$$\mathrm{it}'\mathrm{s}\:\mathrm{all}\:\mathrm{coordinate}\:\mathrm{method}\:\mathrm{with}\:\mathrm{intersecting} \\ $$$$\mathrm{the}\:\mathrm{circle}\:\mathrm{with}\:\mathrm{lines}\:\mathrm{and}\:\mathrm{lines}\:\mathrm{with}\:\mathrm{lines} \\ $$$$\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{have}\:\mathrm{the}\:\mathrm{nerves}\:\mathrm{to}\:\mathrm{type}\:\mathrm{all}\:\mathrm{the}\:\mathrm{work} \\ $$$$\mathrm{sorry}\:\mathrm{for}\:\mathrm{that} \\ $$$$ \\ $$$${a}=\mid{BC}\mid\:\:{b}=\mid{CA}\mid\:\:{c}=\mid{AB}\mid \\ $$$$\delta=\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)} \\ $$$${A}'=\begin{pmatrix}{\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} −\mathrm{3}{c}^{\mathrm{2}} }{\mathrm{6}{c}}}\\{−\frac{\delta}{\mathrm{6}{c}}}\end{pmatrix}\:\:{B}'=\begin{pmatrix}{\frac{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} +\mathrm{3}{c}^{\mathrm{2}} }{\mathrm{6}{c}}}\\{−\frac{\delta}{\mathrm{6}{c}}}\end{pmatrix}\:\:{C}'=\begin{pmatrix}{\frac{−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{\mathrm{3}{c}}}\\{\frac{\delta}{\mathrm{3}{c}}}\end{pmatrix} \\ $$$${r}_{{I}} =\frac{\delta}{\mathrm{2}\left({a}+{b}+{c}\right)} \\ $$$$\Rightarrow\:{I}'=\begin{pmatrix}{\frac{\left({a}−{b}\right)\left({a}+{b}−\mathrm{3}{c}\right)}{\mathrm{6}{c}}}\\{\frac{\left(−{a}−{b}+\mathrm{2}{c}\right)\delta}{\mathrm{6}{c}\left({a}+{b}+{c}\right)}}\end{pmatrix} \\ $$$$\mathrm{let}\:{I}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{0}}\end{pmatrix} \\ $$$$\Rightarrow \\ $$$${A}=\begin{pmatrix}{\frac{{a}−{b}−{c}}{\mathrm{2}}}\\{−\frac{\delta}{\mathrm{2}\left({a}+{b}+{c}\right)}}\end{pmatrix}\:\:{B}=\begin{pmatrix}{\frac{{a}−{b}+{c}}{\mathrm{2}}}\\{−\frac{\delta}{\mathrm{2}\left({a}+{b}+{c}\right)}}\end{pmatrix}\:\:{C}=\begin{pmatrix}{\frac{{a}+{b}−{c}}{\mathrm{2}}×\frac{−{a}+{b}}{{c}}}\\{\frac{\delta}{\mathrm{2}\left({a}+{b}+{c}\right)}×\frac{{a}+{b}}{{c}}}\end{pmatrix} \\ $$$$\Rightarrow \\ $$$${D}=\begin{pmatrix}{\frac{\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}{\mathrm{4}{ac}}}\\{\frac{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\delta}{\mathrm{4}{ac}\left({a}+{b}+{c}\right)}}\end{pmatrix} \\ $$$${E}=\begin{pmatrix}{−\frac{\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}{\mathrm{4}{bc}}}\\{\frac{\left(−{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)\delta}{\mathrm{4}{bc}\left({a}+{b}+{c}\right)}}\end{pmatrix} \\ $$$${F}=\begin{pmatrix}{\mathrm{0}}\\{−\frac{\delta}{\mathrm{2}\left({a}+{b}+{c}\right)}}\end{pmatrix} \\ $$$$\Rightarrow\:{AD}\cap{BE}\cap{CF}={G} \\ $$$${G}=\begin{pmatrix}{\frac{\left({a}−{b}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}{\mathrm{2}{c}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}\left({ab}+{bc}+{ca}\right)\right)}}\\{\frac{\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} −\mathrm{2}{c}^{\mathrm{3}} −\left({a}+{b}\right)\left({ab}−{c}^{\mathrm{2}} \right)\right)\delta}{\mathrm{2}{c}\left({a}+{b}+{c}\right)\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} −\mathrm{2}\left({ab}+{bc}+{ca}\right)\right)}}\end{pmatrix} \\ $$$$ \\ $$$$\mid{AE}\mid=\mid{AF}\mid=\frac{−{a}+{b}+{c}}{\mathrm{2}} \\ $$$$\mid{BD}\mid=\mid{BF}\mid=\frac{{a}−{b}+{c}}{\mathrm{2}} \\ $$$$\mid{CD}\mid=\mid{CE}\mid=\frac{{a}+{b}−{c}}{\mathrm{2}} \\ $$$$\mid{AD}\mid=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left(−{a}+{b}+{c}\right)\left({a}\left({a}+{b}+{c}\right)−\mathrm{2}\left({b}−{c}\right)^{\mathrm{2}} \right)}{{a}}} \\ $$$$\mid{BE}\mid=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left({a}−{b}+{c}\right)\left({b}\left({a}+{b}+{c}\right)−\mathrm{2}\left({c}−{a}\right)^{\mathrm{2}} \right)}{{b}}} \\ $$$$\mid{CF}\mid=\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\frac{\left({a}+{b}−{c}\right)\left({c}\left({a}+{b}+{c}\right)−\mathrm{2}\left({a}−{b}\right)^{\mathrm{2}} \right)}{{c}}} \\ $$
Commented by ajfour last updated on 20/Jul/19

$${Great}\:{Sir},\:{please}\:{view}\:{my} \\ $$$${vector}\:{treatment}! \\ $$
Commented by mr W last updated on 20/Jul/19

$${how}\:{impressed}\:{to}\:{see}\:{how}\:{you}\:{master} \\ $$$${the}\:{coordinate}\:{method}\:{in}\:{such}\:{a} \\ $$$${perfection}! \\ $$
