
Question Number 64580 by jimful last updated on 19/Jul/19
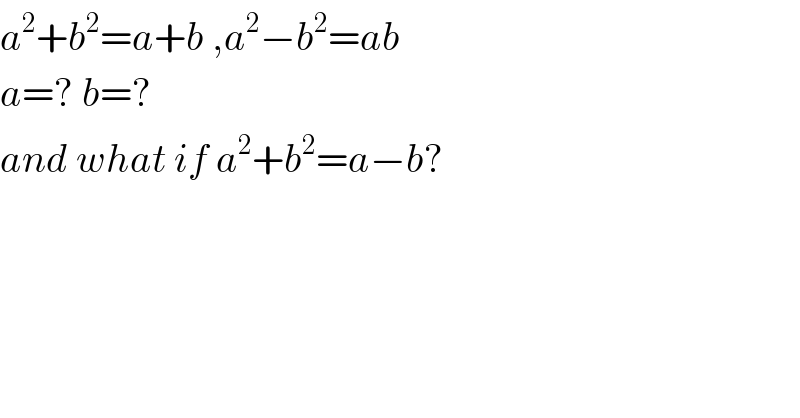
$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={a}+{b}\:,{a}^{\mathrm{2}} −{b}^{\mathrm{2}} ={ab} \\ $$$${a}=?\:{b}=? \\ $$$${and}\:{what}\:{if}\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={a}−{b}? \\ $$
Answered by meme last updated on 19/Jul/19
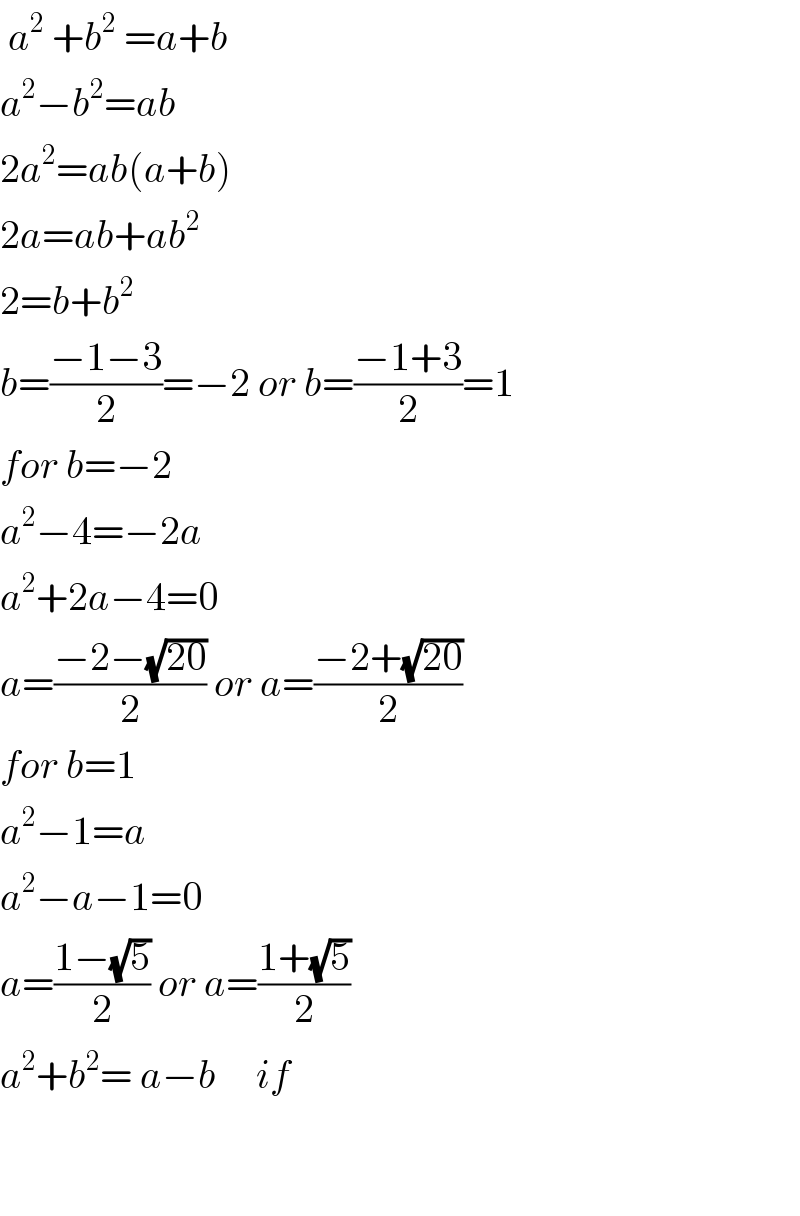
$$\:{a}^{\mathrm{2}} \:+{b}^{\mathrm{2}} \:={a}+{b}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$${a}^{\mathrm{2}} −{b}^{\mathrm{2}} ={ab} \\ $$$$\mathrm{2}{a}^{\mathrm{2}} ={ab}\left({a}+{b}\right) \\ $$$$\mathrm{2}{a}={ab}+{ab}^{\mathrm{2}} \\ $$$$\mathrm{2}={b}+{b}^{\mathrm{2}} \\ $$$${b}=\frac{−\mathrm{1}−\mathrm{3}}{\mathrm{2}}=−\mathrm{2}\:{or}\:{b}=\frac{−\mathrm{1}+\mathrm{3}}{\mathrm{2}}=\mathrm{1} \\ $$$${for}\:{b}=−\mathrm{2} \\ $$$${a}^{\mathrm{2}} −\mathrm{4}=−\mathrm{2}{a} \\ $$$${a}^{\mathrm{2}} +\mathrm{2}{a}−\mathrm{4}=\mathrm{0} \\ $$$${a}=\frac{−\mathrm{2}−\sqrt{\mathrm{20}}}{\mathrm{2}}\:{or}\:{a}=\frac{−\mathrm{2}+\sqrt{\mathrm{20}}}{\mathrm{2}} \\ $$$${for}\:{b}=\mathrm{1} \\ $$$${a}^{\mathrm{2}} −\mathrm{1}={a} \\ $$$${a}^{\mathrm{2}} −{a}−\mathrm{1}=\mathrm{0} \\ $$$${a}=\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:{or}\:{a}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} =\:{a}−{b}\:\:\:\:\:{if} \\ $$$$ \\ $$$$ \\ $$
Answered by MJS last updated on 19/Jul/19
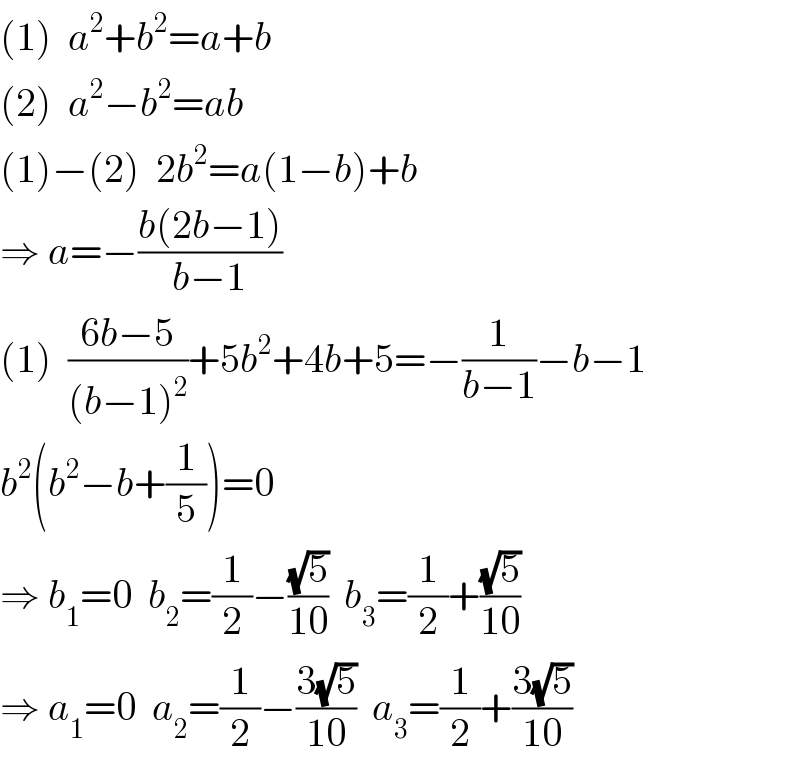
$$\left(\mathrm{1}\right)\:\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={a}+{b} \\ $$$$\left(\mathrm{2}\right)\:\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} ={ab} \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\:\:\mathrm{2}{b}^{\mathrm{2}} ={a}\left(\mathrm{1}−{b}\right)+{b} \\ $$$$\Rightarrow\:{a}=−\frac{{b}\left(\mathrm{2}{b}−\mathrm{1}\right)}{{b}−\mathrm{1}} \\ $$$$\left(\mathrm{1}\right)\:\:\frac{\mathrm{6}{b}−\mathrm{5}}{\left({b}−\mathrm{1}\right)^{\mathrm{2}} }+\mathrm{5}{b}^{\mathrm{2}} +\mathrm{4}{b}+\mathrm{5}=−\frac{\mathrm{1}}{{b}−\mathrm{1}}−{b}−\mathrm{1} \\ $$$${b}^{\mathrm{2}} \left({b}^{\mathrm{2}} −{b}+\frac{\mathrm{1}}{\mathrm{5}}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{b}_{\mathrm{1}} =\mathrm{0}\:\:{b}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{10}}\:\:{b}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{10}} \\ $$$$\Rightarrow\:{a}_{\mathrm{1}} =\mathrm{0}\:\:{a}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{10}}\:\:{a}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{10}} \\ $$
Answered by MJS last updated on 19/Jul/19
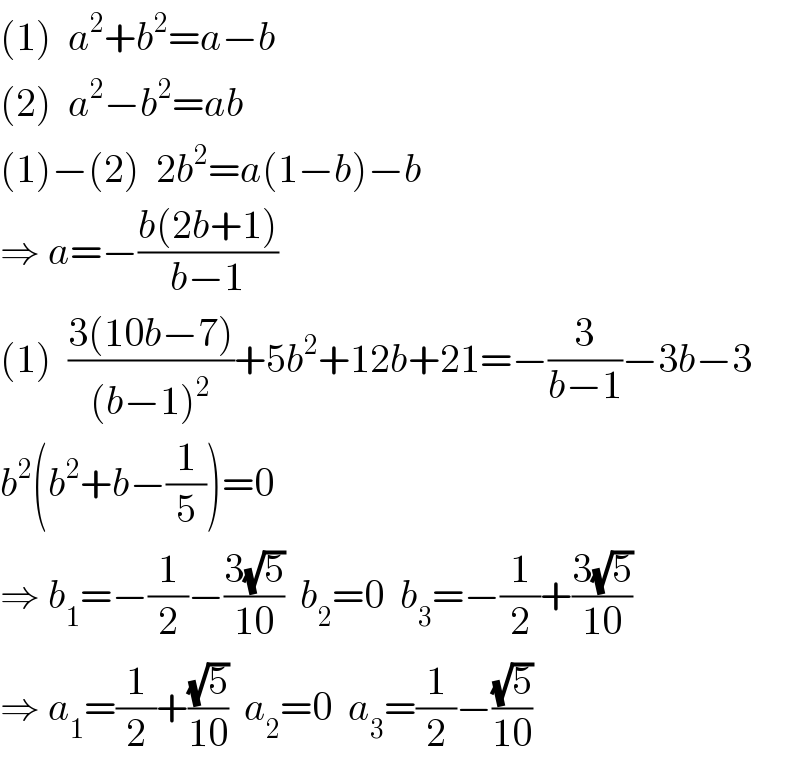
$$\left(\mathrm{1}\right)\:\:{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ={a}−{b} \\ $$$$\left(\mathrm{2}\right)\:\:{a}^{\mathrm{2}} −{b}^{\mathrm{2}} ={ab} \\ $$$$\left(\mathrm{1}\right)−\left(\mathrm{2}\right)\:\:\mathrm{2}{b}^{\mathrm{2}} ={a}\left(\mathrm{1}−{b}\right)−{b} \\ $$$$\Rightarrow\:{a}=−\frac{{b}\left(\mathrm{2}{b}+\mathrm{1}\right)}{{b}−\mathrm{1}} \\ $$$$\left(\mathrm{1}\right)\:\:\frac{\mathrm{3}\left(\mathrm{10}{b}−\mathrm{7}\right)}{\left({b}−\mathrm{1}\right)^{\mathrm{2}} }+\mathrm{5}{b}^{\mathrm{2}} +\mathrm{12}{b}+\mathrm{21}=−\frac{\mathrm{3}}{{b}−\mathrm{1}}−\mathrm{3}{b}−\mathrm{3} \\ $$$${b}^{\mathrm{2}} \left({b}^{\mathrm{2}} +{b}−\frac{\mathrm{1}}{\mathrm{5}}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{b}_{\mathrm{1}} =−\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{10}}\:\:{b}_{\mathrm{2}} =\mathrm{0}\:\:{b}_{\mathrm{3}} =−\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}\sqrt{\mathrm{5}}}{\mathrm{10}} \\ $$$$\Rightarrow\:{a}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{10}}\:\:{a}_{\mathrm{2}} =\mathrm{0}\:\:{a}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{10}} \\ $$
