
Previous in Differential Equation Next in Differential Equation
Question Number 6457 by sanusihammed last updated on 27/Jun/16
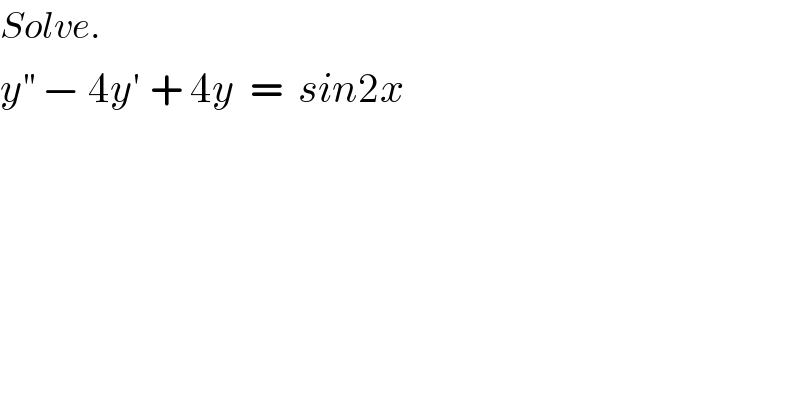
$${Solve}. \\ $$$${y}^{''} \:−\:\mathrm{4}{y}'\:+\:\mathrm{4}{y}\:\:=\:\:{sin}\mathrm{2}{x}\: \\ $$
Answered by nburiburu last updated on 27/Jun/16
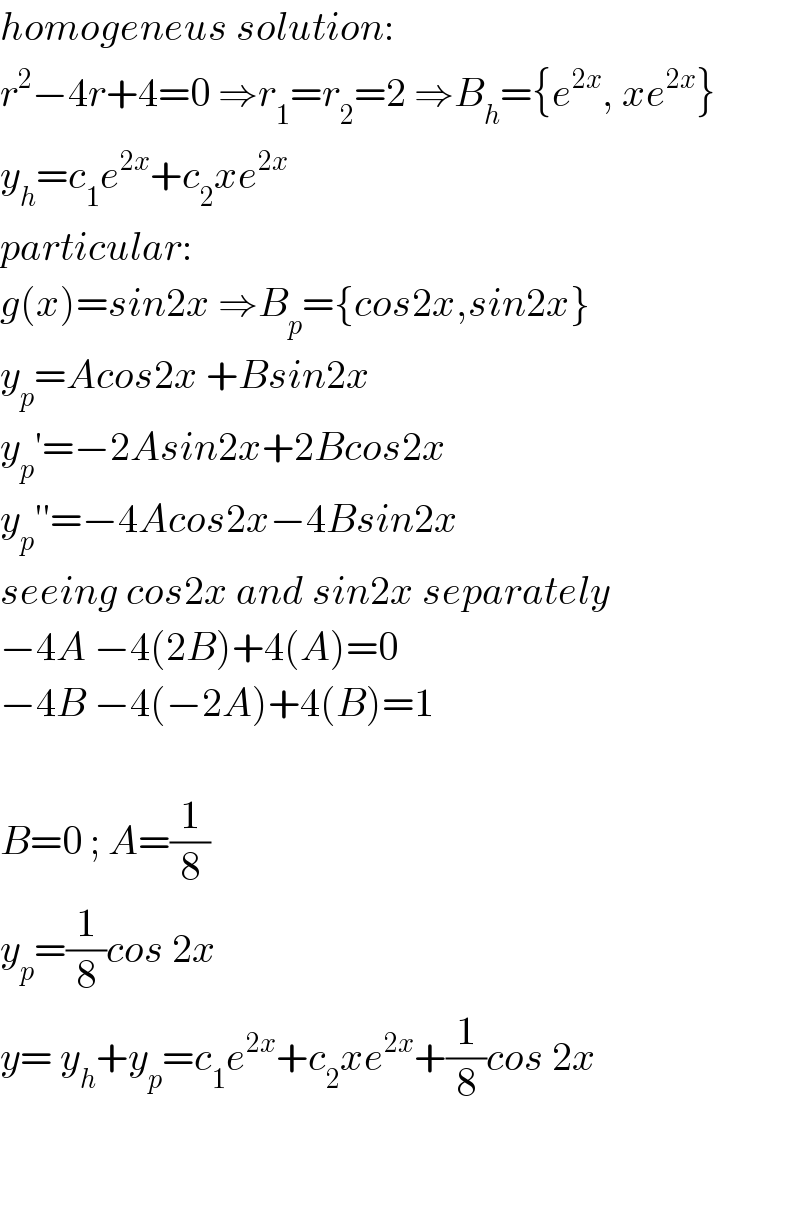
$${homogeneus}\:{solution}: \\ $$$${r}^{\mathrm{2}} −\mathrm{4}{r}+\mathrm{4}=\mathrm{0}\:\Rightarrow{r}_{\mathrm{1}} ={r}_{\mathrm{2}} =\mathrm{2}\:\Rightarrow{B}_{{h}} =\left\{{e}^{\mathrm{2}{x}} ,\:{xe}^{\mathrm{2}{x}} \right\} \\ $$$${y}_{{h}} ={c}_{\mathrm{1}} {e}^{\mathrm{2}{x}} +{c}_{\mathrm{2}} {xe}^{\mathrm{2}{x}} \\ $$$${particular}: \\ $$$${g}\left({x}\right)={sin}\mathrm{2}{x}\:\Rightarrow{B}_{{p}} =\left\{{cos}\mathrm{2}{x},{sin}\mathrm{2}{x}\right\} \\ $$$${y}_{{p}} ={Acos}\mathrm{2}{x}\:+{Bsin}\mathrm{2}{x} \\ $$$${y}_{{p}} '=−\mathrm{2}{Asin}\mathrm{2}{x}+\mathrm{2}{Bcos}\mathrm{2}{x} \\ $$$${y}_{{p}} ''=−\mathrm{4}{Acos}\mathrm{2}{x}−\mathrm{4}{Bsin}\mathrm{2}{x} \\ $$$${seeing}\:{cos}\mathrm{2}{x}\:{and}\:{sin}\mathrm{2}{x}\:{separately} \\ $$$$−\mathrm{4}{A}\:−\mathrm{4}\left(\mathrm{2}{B}\right)+\mathrm{4}\left({A}\right)=\mathrm{0} \\ $$$$−\mathrm{4}{B}\:−\mathrm{4}\left(−\mathrm{2}{A}\right)+\mathrm{4}\left({B}\right)=\mathrm{1} \\ $$$$ \\ $$$${B}=\mathrm{0}\:;\:{A}=\frac{\mathrm{1}}{\mathrm{8}} \\ $$$${y}_{{p}} =\frac{\mathrm{1}}{\mathrm{8}}{cos}\:\mathrm{2}{x} \\ $$$${y}=\:{y}_{{h}} +{y}_{{p}} ={c}_{\mathrm{1}} {e}^{\mathrm{2}{x}} +{c}_{\mathrm{2}} {xe}^{\mathrm{2}{x}} +\frac{\mathrm{1}}{\mathrm{8}}{cos}\:\mathrm{2}{x} \\ $$$$ \\ $$$$ \\ $$
Commented by sanusihammed last updated on 27/Jun/16

$${Wow}\:{thanks}. \\ $$
