
Question Number 64557 by LPM last updated on 19/Jul/19
Commented by LPM last updated on 19/Jul/19

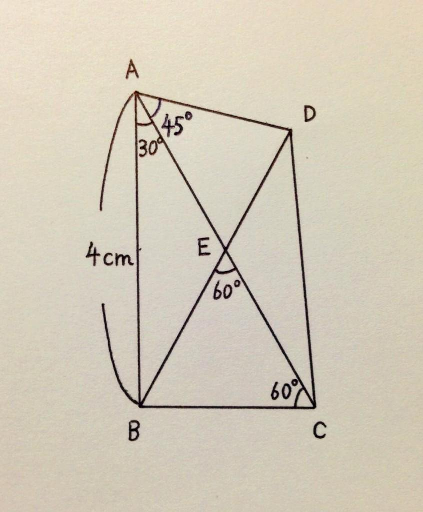
$$\mathrm{area}\:\mathrm{of}\:\bigtriangleup\:\mathrm{DBC}\: \\ $$$$ \\ $$
Commented by Tony Lin last updated on 19/Jul/19

$$\angle{AEB}=\mathrm{120}°\Rightarrow\angle{EBA}=\mathrm{30}° \\ $$$$\angle{EBC}=\mathrm{60}°\Rightarrow\angle{ABC}=\mathrm{90}° \\ $$$$\therefore\bigtriangleup{ABC}\:{is}\:\mathrm{30}°-\mathrm{60}°-\mathrm{90}°\:{triangle} \\ $$$$\Rightarrow{BC}=\frac{\mathrm{4}}{\sqrt{\mathrm{3}}} \\ $$$$\because\bigtriangleup{EBC}\:{is}\:{equilateral}\:{triangle}\:{and} \\ $$$$\:\:\:\bigtriangleup{AEB}\:{is}\:{isosceles}\:{triangle} \\ $$$$\therefore{AE}={EB}={EC}=\frac{\mathrm{4}}{\sqrt{\mathrm{3}}} \\ $$$$\angle{AED}=\mathrm{60}°\Rightarrow\angle{ADE}=\mathrm{75}° \\ $$$$\frac{{AE}}{{sin}\mathrm{75}°}=\frac{{DE}}{{sin}\mathrm{45}°} \\ $$$$\frac{\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}}{\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}}}=\frac{{DE}}{\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}} \\ $$$$\Rightarrow{DE}=\frac{\mathrm{4}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}{\mathrm{3}} \\ $$$${area}\:{of}\:\bigtriangleup{DBC} \\ $$$$=\bigtriangleup{DEC}+\bigtriangleup{EBC} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×{DE}×{EC}×{sin}\angle{DEC}+\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}×{EC}^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{4}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}{\mathrm{3}}×\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}×\left(\frac{\mathrm{4}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{4} \\ $$
Commented by LPM last updated on 19/Jul/19

$$\mathrm{good} \\ $$
Answered by Kunal12588 last updated on 19/Jul/19
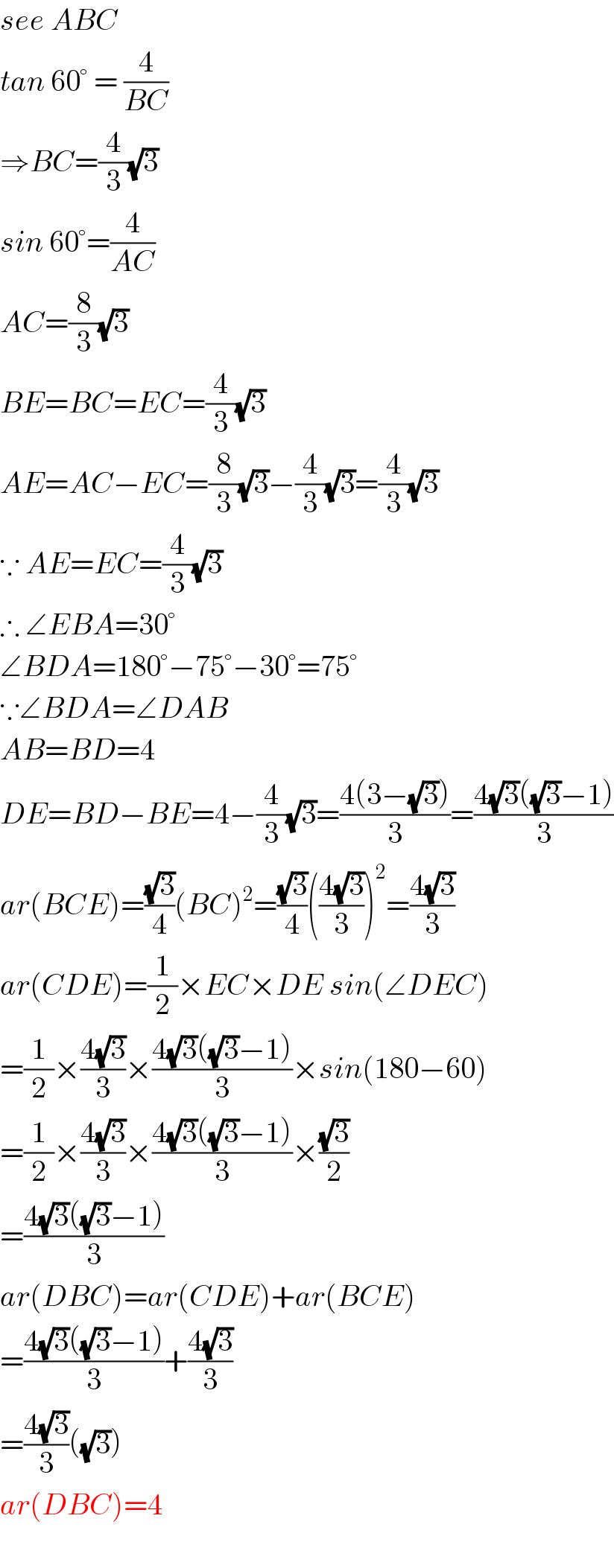
$${see}\:{ABC} \\ $$$${tan}\:\mathrm{60}°\:=\:\frac{\mathrm{4}}{{BC}} \\ $$$$\Rightarrow{BC}=\frac{\mathrm{4}}{\mathrm{3}}\sqrt{\mathrm{3}} \\ $$$${sin}\:\mathrm{60}°=\frac{\mathrm{4}}{{AC}} \\ $$$${AC}=\frac{\mathrm{8}}{\mathrm{3}}\sqrt{\mathrm{3}} \\ $$$${BE}={BC}={EC}=\frac{\mathrm{4}}{\mathrm{3}}\sqrt{\mathrm{3}} \\ $$$${AE}={AC}−{EC}=\frac{\mathrm{8}}{\mathrm{3}}\sqrt{\mathrm{3}}−\frac{\mathrm{4}}{\mathrm{3}}\sqrt{\mathrm{3}}=\frac{\mathrm{4}}{\mathrm{3}}\sqrt{\mathrm{3}} \\ $$$$\because\:{AE}={EC}=\frac{\mathrm{4}}{\mathrm{3}}\sqrt{\mathrm{3}} \\ $$$$\therefore\:\angle{EBA}=\mathrm{30}° \\ $$$$\angle{BDA}=\mathrm{180}°−\mathrm{75}°−\mathrm{30}°=\mathrm{75}° \\ $$$$\because\angle{BDA}=\angle{DAB} \\ $$$${AB}={BD}=\mathrm{4} \\ $$$${DE}={BD}−{BE}=\mathrm{4}−\frac{\mathrm{4}}{\mathrm{3}}\sqrt{\mathrm{3}}=\frac{\mathrm{4}\left(\mathrm{3}−\sqrt{\mathrm{3}}\right)}{\mathrm{3}}=\frac{\mathrm{4}\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{3}} \\ $$$${ar}\left({BCE}\right)=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left({BC}\right)^{\mathrm{2}} =\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}\left(\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}}\right)^{\mathrm{2}} =\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$${ar}\left({CDE}\right)=\frac{\mathrm{1}}{\mathrm{2}}×{EC}×{DE}\:{sin}\left(\angle{DEC}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}}×\frac{\mathrm{4}\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{3}}×{sin}\left(\mathrm{180}−\mathrm{60}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}}×\frac{\mathrm{4}\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{3}} \\ $$$${ar}\left({DBC}\right)={ar}\left({CDE}\right)+{ar}\left({BCE}\right) \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{3}}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)}{\mathrm{3}}+\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$=\frac{\mathrm{4}\sqrt{\mathrm{3}}}{\mathrm{3}}\left(\sqrt{\mathrm{3}}\right) \\ $$$${ar}\left({DBC}\right)=\mathrm{4} \\ $$$$ \\ $$
Commented by LPM last updated on 19/Jul/19

$$\mathrm{good} \\ $$
