
Question Number 64350 by Rio Michael last updated on 16/Jul/19
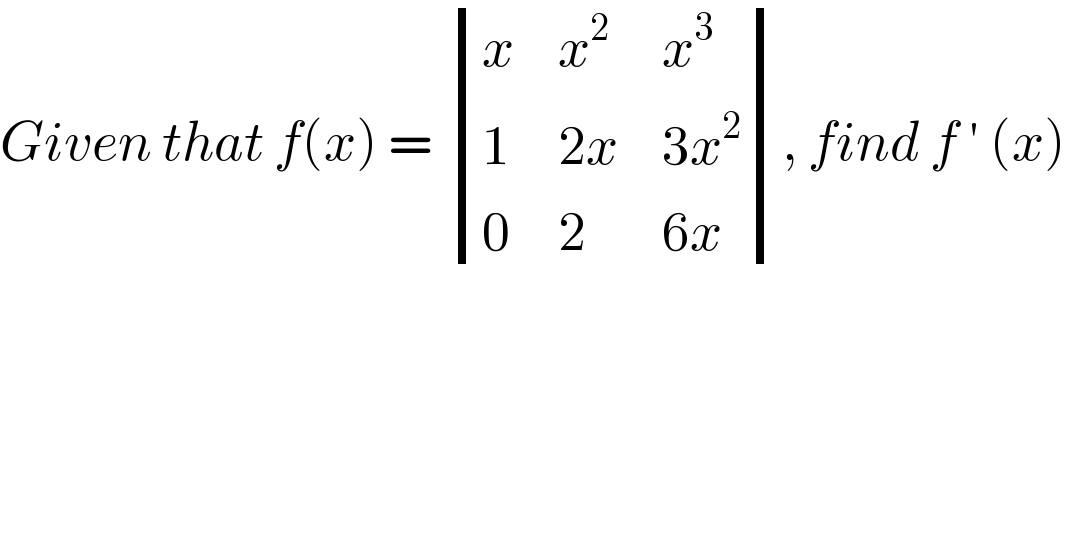
$${Given}\:{that}\:{f}\left({x}\right)\:=\:\begin{vmatrix}{{x}}&{{x}^{\mathrm{2}} }&{{x}^{\mathrm{3}} }\\{\mathrm{1}}&{\mathrm{2}{x}}&{\mathrm{3}{x}^{\mathrm{2}} }\\{\mathrm{0}}&{\mathrm{2}}&{\mathrm{6}{x}}\end{vmatrix},\:{find}\:{f}\:'\:\left({x}\right) \\ $$
Commented by Tony Lin last updated on 17/Jul/19
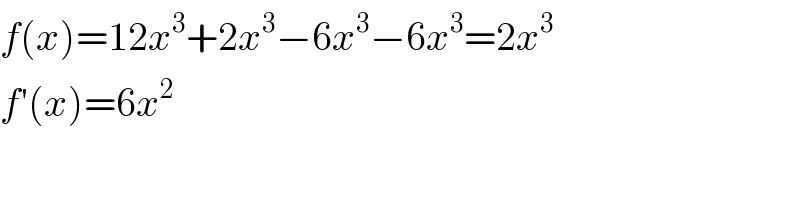
$${f}\left({x}\right)=\mathrm{12}{x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{3}} =\mathrm{2}{x}^{\mathrm{3}} \\ $$$${f}'\left({x}\right)=\mathrm{6}{x}^{\mathrm{2}} \\ $$
Commented by Rio Michael last updated on 17/Jul/19

$${thanks} \\ $$
Commented by Prithwish sen last updated on 17/Jul/19
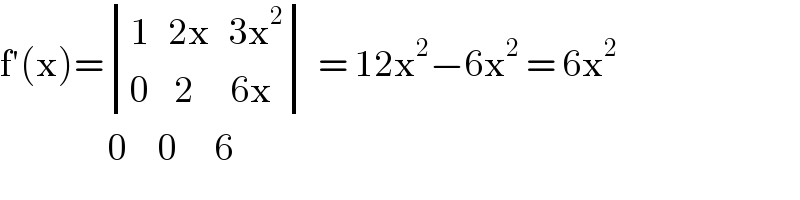
$$\mathrm{f}'\left(\mathrm{x}\right)=\begin{vmatrix}{\mathrm{1}\:\:\:\mathrm{2x}\:\:\:\mathrm{3x}^{\mathrm{2}} }\\{\mathrm{0}\:\:\:\:\mathrm{2}\:\:\:\:\:\:\mathrm{6x}}\end{vmatrix}\:=\:\mathrm{12x}^{\mathrm{2}} −\mathrm{6x}^{\mathrm{2}} \:=\:\mathrm{6x}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\mathrm{6} \\ $$
