
Question Number 64268 by Chi Mes Try last updated on 16/Jul/19
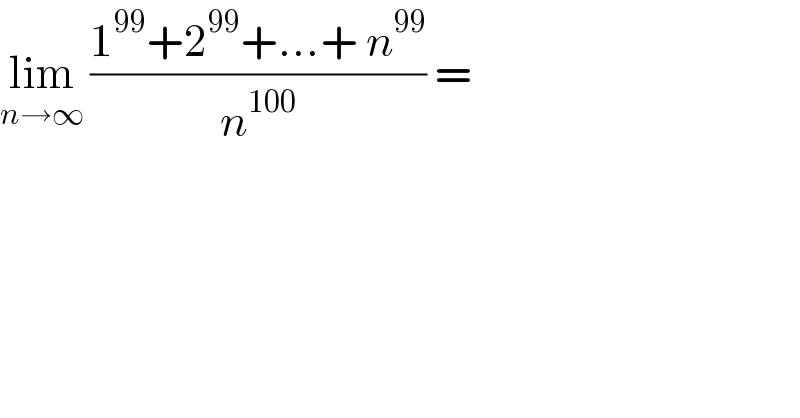
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\frac{\mathrm{1}^{\mathrm{99}} +\mathrm{2}^{\mathrm{99}} +...+\:{n}^{\mathrm{99}} }{{n}^{\mathrm{100}} }\:= \\ $$
Commented by Prithwish sen last updated on 16/Jul/19
![lim_(n−→∞) (1/n)Σ_(r=1) ^n ((r/n))^(99) = ∫_0 ^1 x^(99) dx =[ (x^(100) /(100))]_0 ^1 = (1/(100))](Q64275.png)
$$\mathrm{lim}_{\mathrm{n}−\rightarrow\infty} \frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\left(\frac{\mathrm{r}}{\mathrm{n}}\right)^{\mathrm{99}} \\ $$$$=\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\mathrm{99}} \mathrm{dx} \\ $$$$=\left[\:\frac{\mathrm{x}^{\mathrm{100}} }{\mathrm{100}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\:\frac{\mathrm{1}}{\mathrm{100}} \\ $$
