
Question Number 64267 by Chi Mes Try last updated on 16/Jul/19
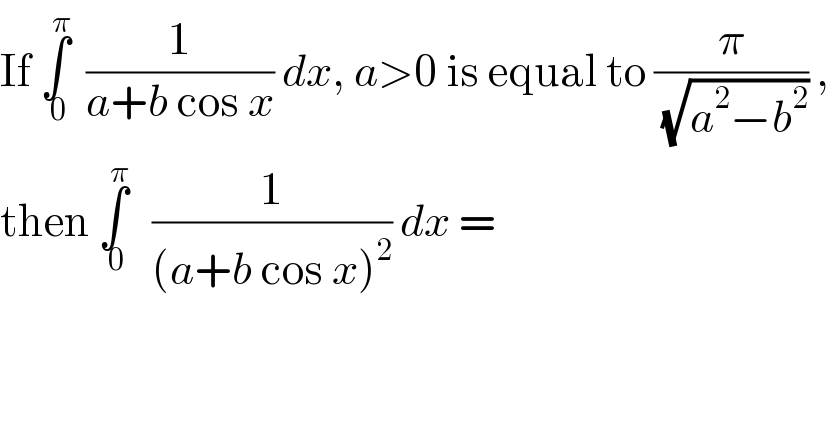
$$\mathrm{If}\:\underset{\:\mathrm{0}} {\overset{\pi} {\int}}\:\:\frac{\mathrm{1}}{{a}+{b}\:\mathrm{cos}\:{x}}\:{dx},\:{a}>\mathrm{0}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to}\:\frac{\pi}{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}\:, \\ $$ $$\mathrm{then}\:\underset{\:\mathrm{0}} {\overset{\pi} {\int}}\:\:\:\frac{\mathrm{1}}{\left({a}+{b}\:\mathrm{cos}\:{x}\right)^{\mathrm{2}} }\:{dx}\:= \\ $$
Commented byPrithwish sen last updated on 16/Jul/19
![∫_0 ^π (d/da)[(1/(a+bcosx))]dx =(d/da) (π/(√(a^2 −b^2 ))) ∫_0 ^π (dx/((1+cosx)^2 )) = ((aπ)/((a^2 −b^2 )^(3/2) )) please check.](Q64280.png)
$$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{d}}{\mathrm{da}}\left[\frac{\mathrm{1}}{\mathrm{a}+\mathrm{bcosx}}\right]\mathrm{dx}\:=\frac{\mathrm{d}}{\mathrm{da}}\:\frac{\pi}{\sqrt{\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} }} \\ $$ $$\int_{\mathrm{0}} ^{\pi} \frac{\mathrm{dx}}{\left(\mathrm{1}+\mathrm{cosx}\right)^{\mathrm{2}} }\:=\:\frac{\mathrm{a}\pi}{\left(\mathrm{a}^{\mathrm{2}} −\mathrm{b}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\:\:\mathrm{please}\:\mathrm{check}. \\ $$
Answered by Tanmay chaudhury last updated on 16/Jul/19
![∫_0 ^π (dx/(a(sin^2 (x/2)+cos^2 (x/2))+b(cos^2 (x/2)−sin^2 (x/2)))) ∫_0 ^π (dx/((a+b)cos^2 (x/2)+(a−b)sin^2 (x/2))) ∫_0 ^π ((sec^2 (x/2))/((a+b)+(a−b)tan^2 (x/2))) (1/(a−b))∫_0 ^π ((sec^2 (x/2)dx)/(((√((a+b)/(a−b))) )^2 +tan^2 (x/2))) p=tan(x/2) (dp/dx)=sec^2 (x/2)×(1/2) (1/(a−b))∫_0 ^∞ ((2dp)/(((√((a+b)/(a−b))) )^2 +p^2 )) (2/(a−b))×(1/(√((a+b)/(a−b))))∣tan^(−1) ((p/((√((a+b)/(a−b))) )))∣_0 ^∞ =(2/(√(a^2 −b^2 )))×[tan^(−1) (∞)] =(π/(√(a^2 −b^2 ))) I(a,b)=∫_0 ^π (dx/(a+bcosx))=(π/(√(a^2 −b^2 ))) (dI/da)=∫_0 ^π (∂/∂a)((1/(a+bcosx)))dx=π(∂/∂a){(a^2 −b^2 )^((−1)/2) } (dI/da)=∫_0 ^π ((−1)/((a+bcosx)^2 ))×(1+0)dx=((−π)/2)×(a^2 −b^2 )^((−3)/2) ×2a so∫_0 ^π ((−dx)/((a+bcosx)^2 ))=((−πa)/((a^2 −b^2 )^(3/2) )) so ∫_0 ^π (dx/((a+bcosx)^2 ))=((πa)/((a^2 −b^2 )^(3/2) )) Tanmay 16.07.19](Q64301.png)
$$\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{{a}\left({sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right)+{b}\left({cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}−{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}\right)} \\ $$ $$\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\left({a}+{b}\right){cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\left({a}−{b}\right){sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$ $$\int_{\mathrm{0}} ^{\pi} \frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}}{\left({a}+{b}\right)+\left({a}−{b}\right){tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$ $$\frac{\mathrm{1}}{{a}−{b}}\int_{\mathrm{0}} ^{\pi} \frac{{sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}{dx}}{\left(\sqrt{\frac{{a}+{b}}{{a}−{b}}}\:\right)^{\mathrm{2}} +{tan}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}} \\ $$ $${p}={tan}\frac{{x}}{\mathrm{2}}\:\:\:\frac{{dp}}{{dx}}={sec}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}×\frac{\mathrm{1}}{\mathrm{2}} \\ $$ $$\frac{\mathrm{1}}{{a}−{b}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{2}{dp}}{\left(\sqrt{\frac{{a}+{b}}{{a}−{b}}}\:\right)^{\mathrm{2}} +{p}^{\mathrm{2}} } \\ $$ $$\frac{\mathrm{2}}{{a}−{b}}×\frac{\mathrm{1}}{\sqrt{\frac{{a}+{b}}{{a}−{b}}}}\mid{tan}^{−\mathrm{1}} \left(\frac{{p}}{\sqrt{\frac{{a}+{b}}{{a}−{b}}}\:}\right)\mid_{\mathrm{0}} ^{\infty} \\ $$ $$=\frac{\mathrm{2}}{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }}×\left[{tan}^{−\mathrm{1}} \left(\infty\right)\right] \\ $$ $$=\frac{\pi}{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }} \\ $$ $${I}\left({a},{b}\right)=\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{{a}+{bcosx}}=\frac{\pi}{\sqrt{{a}^{\mathrm{2}} −{b}^{\mathrm{2}} }} \\ $$ $$\frac{{dI}}{{da}}=\int_{\mathrm{0}} ^{\pi} \frac{\partial}{\partial{a}}\left(\frac{\mathrm{1}}{{a}+{bcosx}}\right){dx}=\pi\frac{\partial}{\partial{a}}\left\{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\frac{−\mathrm{1}}{\mathrm{2}}} \right\} \\ $$ $$\frac{{dI}}{{da}}=\int_{\mathrm{0}} ^{\pi} \frac{−\mathrm{1}}{\left({a}+{bcosx}\right)^{\mathrm{2}} }×\left(\mathrm{1}+\mathrm{0}\right){dx}=\frac{−\pi}{\mathrm{2}}×\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\frac{−\mathrm{3}}{\mathrm{2}}} ×\mathrm{2}{a} \\ $$ $${so}\int_{\mathrm{0}} ^{\pi} \frac{−{dx}}{\left({a}+{bcosx}\right)^{\mathrm{2}} }=\frac{−\pi{a}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$ $${so}\:\int_{\mathrm{0}} ^{\pi} \frac{{dx}}{\left({a}+{bcosx}\right)^{\mathrm{2}} }=\frac{\pi{a}}{\left({a}^{\mathrm{2}} −{b}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\:} \\ $$ $${Tanmay}\:\:\mathrm{16}.\mathrm{07}.\mathrm{19} \\ $$
