
Question Number 64227 by Tony Lin last updated on 16/Jul/19
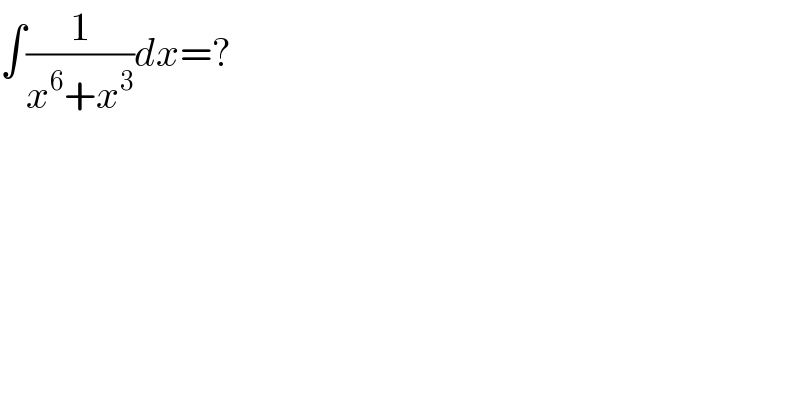
$$\int\frac{\mathrm{1}}{{x}^{\mathrm{6}} +{x}^{\mathrm{3}} }{dx}=? \\ $$
Answered by ajfour last updated on 16/Jul/19
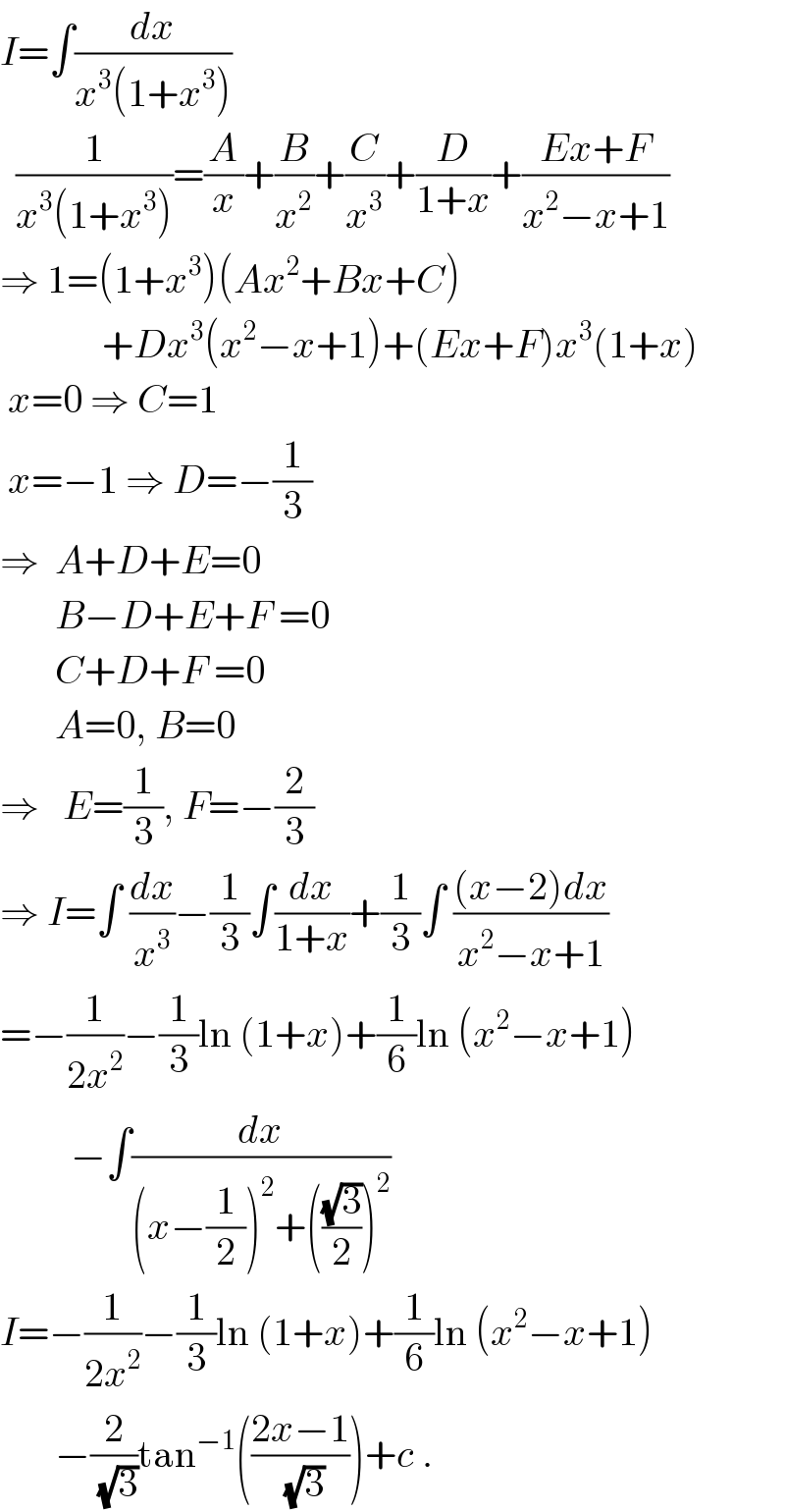
$${I}=\int\frac{{dx}}{{x}^{\mathrm{3}} \left(\mathrm{1}+{x}^{\mathrm{3}} \right)} \\ $$$$\:\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} \left(\mathrm{1}+{x}^{\mathrm{3}} \right)}=\frac{{A}}{{x}}+\frac{{B}}{{x}^{\mathrm{2}} }+\frac{{C}}{{x}^{\mathrm{3}} }+\frac{{D}}{\mathrm{1}+{x}}+\frac{{Ex}+{F}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$\Rightarrow\:\mathrm{1}=\left(\mathrm{1}+{x}^{\mathrm{3}} \right)\left({Ax}^{\mathrm{2}} +{Bx}+{C}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:+{Dx}^{\mathrm{3}} \left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)+\left({Ex}+{F}\right){x}^{\mathrm{3}} \left(\mathrm{1}+{x}\right) \\ $$$$\:{x}=\mathrm{0}\:\Rightarrow\:{C}=\mathrm{1}\: \\ $$$$\:{x}=−\mathrm{1}\:\Rightarrow\:{D}=−\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\Rightarrow\:\:{A}+{D}+{E}=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{B}−{D}+{E}+{F}\:=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{C}+{D}+{F}\:=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:{A}=\mathrm{0},\:{B}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{E}=\frac{\mathrm{1}}{\mathrm{3}},\:{F}=−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow\:{I}=\int\:\frac{{dx}}{{x}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\mathrm{1}+{x}}+\frac{\mathrm{1}}{\mathrm{3}}\int\:\frac{\left({x}−\mathrm{2}\right){dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\left(\mathrm{1}+{x}\right)+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:−\int\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)^{\mathrm{2}} } \\ $$$${I}=−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\left(\mathrm{1}+{x}\right)+\frac{\mathrm{1}}{\mathrm{6}}\mathrm{ln}\:\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:−\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)+{c}\:. \\ $$
Commented by Tony Lin last updated on 16/Jul/19

$${thanks}\:{sir} \\ $$
