
Question Number 64186 by Hope last updated on 15/Jul/19
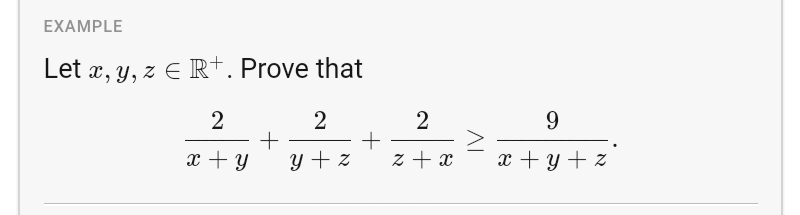
Answered by Hope last updated on 15/Jul/19
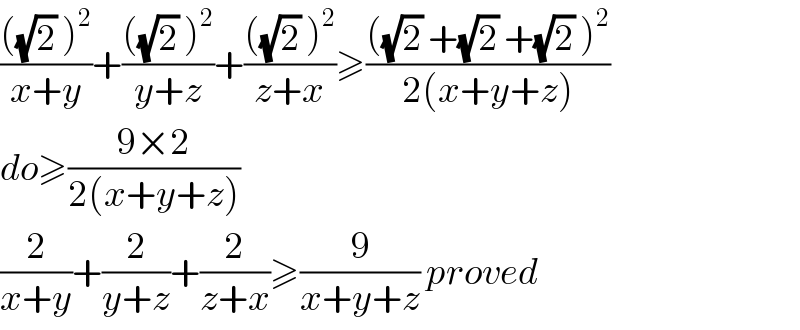
$$\frac{\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} }{{x}+{y}}+\frac{\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} }{{y}+{z}}+\frac{\left(\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} }{{z}+{x}}\geqslant\frac{\left(\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} }{\mathrm{2}\left({x}+{y}+{z}\right)} \\ $$$${do}\geqslant\frac{\mathrm{9}×\mathrm{2}}{\mathrm{2}\left({x}+{y}+{z}\right)} \\ $$$$\frac{\mathrm{2}}{{x}+{y}}+\frac{\mathrm{2}}{{y}+{z}}+\frac{\mathrm{2}}{{z}+{x}}\geqslant\frac{\mathrm{9}}{{x}+{y}+{z}}\:{proved} \\ $$
