
Question Number 63941 by gunawan last updated on 11/Jul/19

$$\mathrm{If}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the}\:\mathrm{coefficients}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion} \\ $$$$\mathrm{of}\:\left(\mathrm{1}−\mathrm{3}{x}+\mathrm{10}{x}^{\mathrm{2}} \right)^{{n}} \:\mathrm{is}\:\:{a}\:\mathrm{and}\:\mathrm{if}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{coefficients}\:\mathrm{in}\:\mathrm{the}\:\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}} \:\mathrm{is} \\ $$$${b},\:\mathrm{then} \\ $$
Answered by mr W last updated on 11/Jul/19
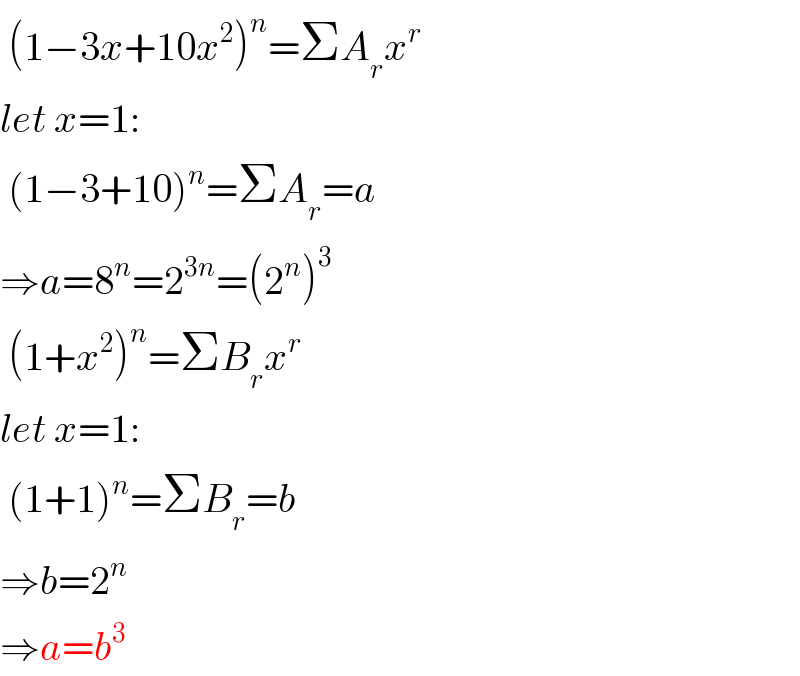
$$\:\left(\mathrm{1}−\mathrm{3}{x}+\mathrm{10}{x}^{\mathrm{2}} \right)^{{n}} =\Sigma{A}_{{r}} {x}^{{r}} \\ $$$${let}\:{x}=\mathrm{1}: \\ $$$$\:\left(\mathrm{1}−\mathrm{3}+\mathrm{10}\right)^{{n}} =\Sigma{A}_{{r}} ={a} \\ $$$$\Rightarrow{a}=\mathrm{8}^{{n}} =\mathrm{2}^{\mathrm{3}{n}} =\left(\mathrm{2}^{{n}} \right)^{\mathrm{3}} \\ $$$$\:\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{{n}} =\Sigma{B}_{{r}} {x}^{{r}} \\ $$$${let}\:{x}=\mathrm{1}: \\ $$$$\:\left(\mathrm{1}+\mathrm{1}\right)^{{n}} =\Sigma{B}_{{r}} ={b} \\ $$$$\Rightarrow{b}=\mathrm{2}^{{n}} \\ $$$$\Rightarrow{a}={b}^{\mathrm{3}} \\ $$
