
Question Number 6390 by FilupSmith last updated on 25/Jun/16
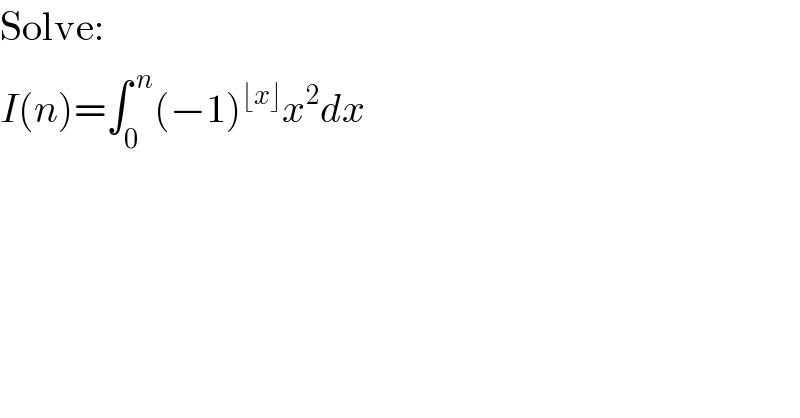
$$\mathrm{Solve}: \\ $$$${I}\left({n}\right)=\int_{\mathrm{0}} ^{\:{n}} \left(−\mathrm{1}\right)^{\lfloor{x}\rfloor} {x}^{\mathrm{2}} {dx} \\ $$
Commented by prakash jain last updated on 25/Jun/16
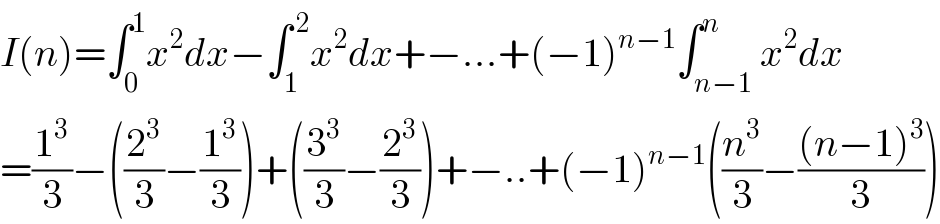
$${I}\left({n}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} {dx}−\int_{\mathrm{1}} ^{\:\mathrm{2}} {x}^{\mathrm{2}} {dx}+−...+\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \int_{{n}−\mathrm{1}} ^{{n}} {x}^{\mathrm{2}} {dx} \\ $$$$=\frac{\mathrm{1}^{\mathrm{3}} }{\mathrm{3}}−\left(\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{1}^{\mathrm{3}} }{\mathrm{3}}\right)+\left(\frac{\mathrm{3}^{\mathrm{3}} }{\mathrm{3}}−\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}}\right)+−..+\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \left(\frac{{n}^{\mathrm{3}} }{\mathrm{3}}−\frac{\left({n}−\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{3}}\right) \\ $$
Commented by FilupSmith last updated on 26/Jun/16
$$\mathrm{I}\:\mathrm{love}\:\mathrm{this}\:\mathrm{approach}!\:\mathrm{i}\:\mathrm{didnt}\:\mathrm{even}\:\mathrm{think} \\ $$$$\mathrm{of}\:\mathrm{it}\:\mathrm{this}\:\mathrm{way}! \\ $$
Commented by malwaan last updated on 26/Jun/16
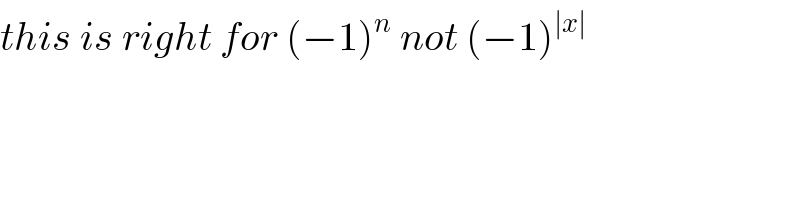
$${this}\:{is}\:{right}\:{for}\:\left(−\mathrm{1}\right)^{{n}} \:{not}\:\left(−\mathrm{1}\right)^{\mid{x}\mid} \\ $$
Commented by prakash jain last updated on 26/Jun/16

$$\lfloor{x}\rfloor \\ $$$$\mathrm{0}\:{for}\:\mathrm{0}\leqslant{x}<\mathrm{1} \\ $$$$\mathrm{1}\:{for}\:\mathrm{1}\leqslant{x}<\mathrm{2} \\ $$$${and}\:{so}\:{on} \\ $$
