
Question Number 63881 by mmkkmm000m last updated on 10/Jul/19
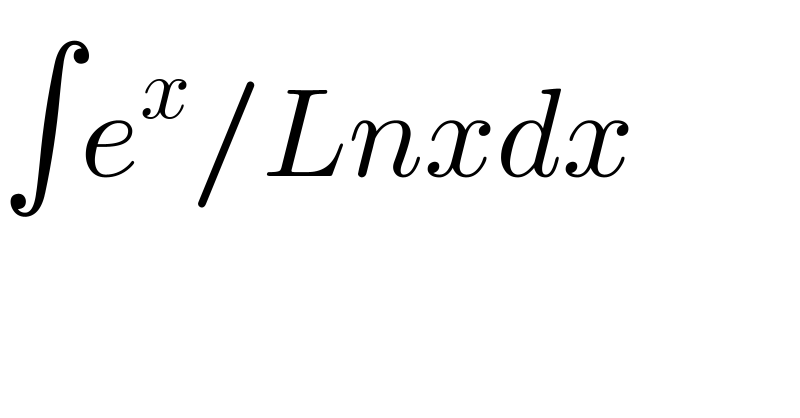
$$\int{e}^{{x}} /{Lnxdx} \\ $$
Commented by mathmax by abdo last updated on 11/Jul/19
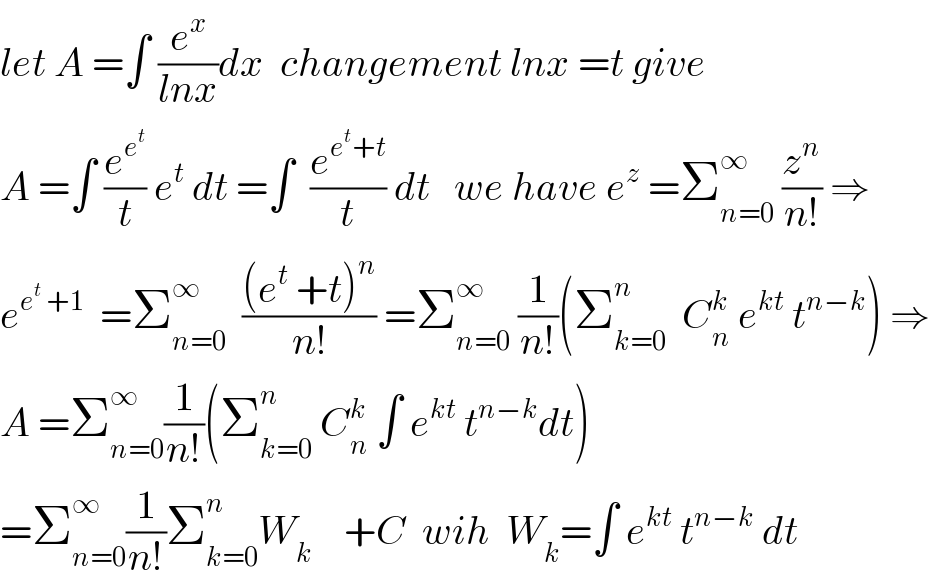
$${let}\:{A}\:=\int\:\frac{{e}^{{x}} }{{lnx}}{dx}\:\:{changement}\:{lnx}\:={t}\:{give} \\ $$$${A}\:=\int\:\frac{{e}^{{e}^{{t}} } }{{t}}\:{e}^{{t}} \:{dt}\:=\int\:\:\frac{{e}^{{e}^{{t}} +{t}} }{{t}}\:{dt}\:\:\:{we}\:{have}\:{e}^{{z}} \:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{z}^{{n}} }{{n}!}\:\Rightarrow \\ $$$${e}^{{e}^{{t}} \:+\mathrm{1}} \:\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\left({e}^{{t}} \:+{t}\right)^{{n}} }{{n}!}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{{n}!}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:\:{C}_{{n}} ^{{k}} \:{e}^{{kt}} \:{t}^{{n}−{k}} \right)\:\Rightarrow \\ $$$${A}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{n}!}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:{C}_{{n}} ^{{k}} \:\int\:{e}^{{kt}} \:{t}^{{n}−{k}} {dt}\right) \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{n}!}\sum_{{k}=\mathrm{0}} ^{{n}} {W}_{{k}} \:\:\:\:+{C}\:\:{wih}\:\:{W}_{{k}} =\int\:{e}^{{kt}} \:{t}^{{n}−{k}} \:{dt} \\ $$
