
Question Number 63861 by gunawan last updated on 10/Jul/19
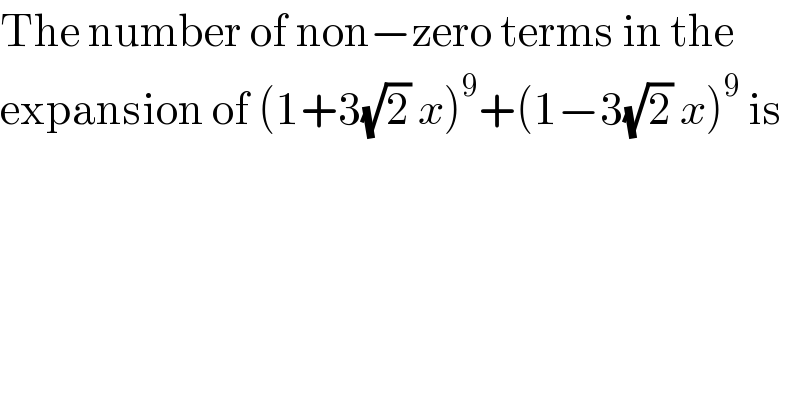
$$\mathrm{The}\:\mathrm{number}\:\mathrm{of}\:\mathrm{non}−\mathrm{zero}\:\mathrm{terms}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{expansion}\:\mathrm{of}\:\left(\mathrm{1}+\mathrm{3}\sqrt{\mathrm{2}}\:{x}\right)^{\mathrm{9}} +\left(\mathrm{1}−\mathrm{3}\sqrt{\mathrm{2}}\:{x}\right)^{\mathrm{9}} \:\mathrm{is} \\ $$
Commented by kaivan.ahmadi last updated on 10/Jul/19
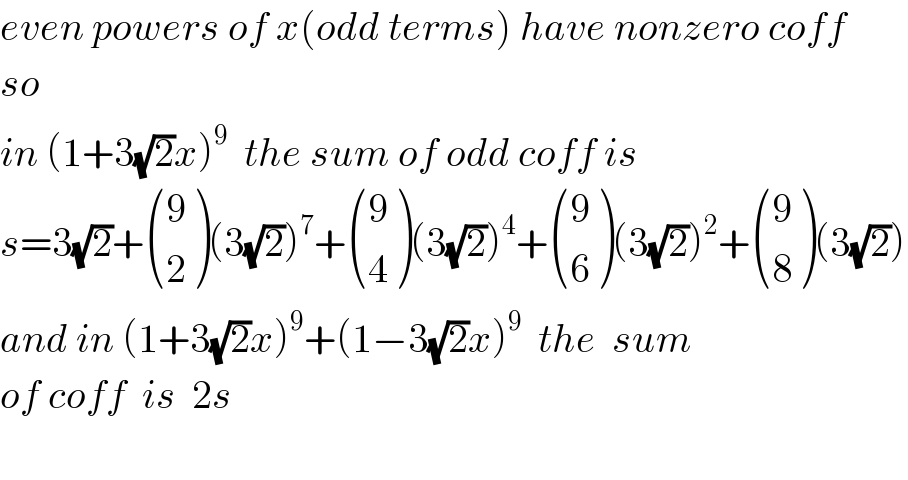
$${even}\:{powers}\:{of}\:{x}\left({odd}\:{terms}\right)\:{have}\:{nonzero}\:{coff} \\ $$$${so} \\ $$$${in}\:\left(\mathrm{1}+\mathrm{3}\sqrt{\mathrm{2}}{x}\right)^{\mathrm{9}} \:\:{the}\:{sum}\:{of}\:{odd}\:{coff}\:{is} \\ $$$${s}=\mathrm{3}\sqrt{\mathrm{2}}+\begin{pmatrix}{\mathrm{9}}\\{\mathrm{2}}\end{pmatrix}\left(\mathrm{3}\sqrt{\mathrm{2}}\right)^{\mathrm{7}} +\begin{pmatrix}{\mathrm{9}}\\{\mathrm{4}}\end{pmatrix}\left(\mathrm{3}\sqrt{\mathrm{2}}\right)^{\mathrm{4}} +\begin{pmatrix}{\mathrm{9}}\\{\mathrm{6}}\end{pmatrix}\left(\mathrm{3}\sqrt{\mathrm{2}}\right)^{\mathrm{2}} +\begin{pmatrix}{\mathrm{9}}\\{\mathrm{8}}\end{pmatrix}\left(\mathrm{3}\sqrt{\mathrm{2}}\right) \\ $$$${and}\:{in}\:\left(\mathrm{1}+\mathrm{3}\sqrt{\mathrm{2}}{x}\right)^{\mathrm{9}} +\left(\mathrm{1}−\mathrm{3}\sqrt{\mathrm{2}}{x}\right)^{\mathrm{9}} \:\:{the}\:\:{sum} \\ $$$${of}\:{coff}\:\:{is}\:\:\mathrm{2}{s} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 10/Jul/19
![we have (1+3(√2)x)^9 +(1−3(√2))^9 =Σ_(k=0) ^9 C_9 ^k (3(√2)x)^k +Σ_(k=0) ^9 C_9 ^k (−1)^k (3(√2))^k =Σ_(k=0) ^9 C_9 ^k (1+(−1)^k )(3(√2))^k x^k =Σ_(p=0) ^([(9/2)]) C_9 ^(2p) 2 ×2^p 3^(2p) x^(2p) =Σ_(p=0) ^4 C_9 ^(2p) 2^(p+1) 9^p x^(2p) Σ_(p=0) ^4 a_p x^(2p) with a_p =2^(p+1) 9^p C_9 ^(2p) we see that a_p ≥0 ....](Q63897.png)
$${we}\:{have}\:\left(\mathrm{1}+\mathrm{3}\sqrt{\mathrm{2}}{x}\right)^{\mathrm{9}} \:+\left(\mathrm{1}−\mathrm{3}\sqrt{\mathrm{2}}\right)^{\mathrm{9}} =\sum_{{k}=\mathrm{0}} ^{\mathrm{9}} \:{C}_{\mathrm{9}} ^{{k}} \left(\mathrm{3}\sqrt{\mathrm{2}}{x}\right)^{{k}} \\ $$$$+\sum_{{k}=\mathrm{0}} ^{\mathrm{9}} \:{C}_{\mathrm{9}} ^{{k}} \:\left(−\mathrm{1}\right)^{{k}} \left(\mathrm{3}\sqrt{\mathrm{2}}\right)^{{k}} \:=\sum_{{k}=\mathrm{0}} ^{\mathrm{9}} {C}_{\mathrm{9}} ^{{k}} \left(\mathrm{1}+\left(−\mathrm{1}\right)^{{k}} \right)\left(\mathrm{3}\sqrt{\mathrm{2}}\right)^{{k}} \:{x}^{{k}} \\ $$$$=\sum_{{p}=\mathrm{0}} ^{\left[\frac{\mathrm{9}}{\mathrm{2}}\right]} \:{C}_{\mathrm{9}} ^{\mathrm{2}{p}} \:\:\mathrm{2}\:\:×\mathrm{2}^{{p}} \:\mathrm{3}^{\mathrm{2}{p}} \:{x}^{\mathrm{2}{p}} \:=\sum_{{p}=\mathrm{0}} ^{\mathrm{4}} \:{C}_{\mathrm{9}} ^{\mathrm{2}{p}} \:\mathrm{2}^{{p}+\mathrm{1}} \:\mathrm{9}^{{p}} \:{x}^{\mathrm{2}{p}} \: \\ $$$$\sum_{{p}=\mathrm{0}} ^{\mathrm{4}} \:{a}_{{p}} \:\:{x}^{\mathrm{2}{p}} \:\:{with}\:{a}_{{p}} =\mathrm{2}^{{p}+\mathrm{1}} \:\mathrm{9}^{{p}} \:{C}_{\mathrm{9}} ^{\mathrm{2}{p}} \:{we}\:{see}\:{that}\:{a}_{{p}} \geqslant\mathrm{0}\:.... \\ $$
