
Question Number 63812 by kaivan.ahmadi last updated on 09/Jul/19

$$ \\ $$$${A}\:\:{can}\:{terminate}\:{a}\:{work}\:\:\mathrm{9}\:{hour}\:{earlier} \\ $$$${than}\:{B}. \\ $$$${A}\:\:{and}\:\:{B}\:\:{terminate}\:{that}\:{work}\:\:{after}\:\mathrm{20}\:{hour}\:{together}. \\ $$$${A}\:{can}\:{terminate}\:{that}\:{work}\:{after}\:....\:{hour}. \\ $$$$ \\ $$$$ \\ $$
Commented by kaivan.ahmadi last updated on 09/Jul/19
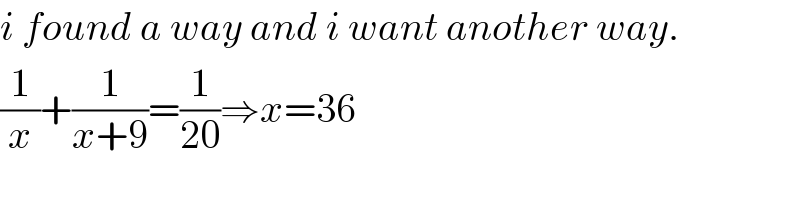
$${i}\:{found}\:{a}\:{way}\:{and}\:{i}\:{want}\:{another}\:{way}. \\ $$$$\frac{\mathrm{1}}{{x}}+\frac{\mathrm{1}}{{x}+\mathrm{9}}=\frac{\mathrm{1}}{\mathrm{20}}\Rightarrow{x}=\mathrm{36} \\ $$
Commented by MJS last updated on 09/Jul/19
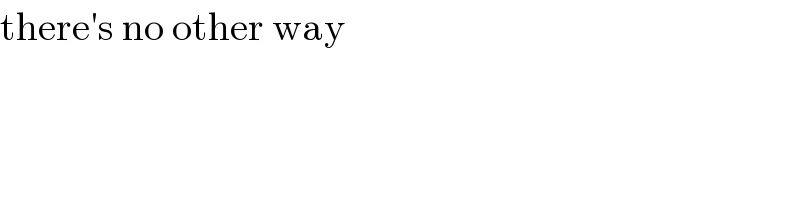
$$\mathrm{there}'\mathrm{s}\:\mathrm{no}\:\mathrm{other}\:\mathrm{way} \\ $$
