
Question Number 63722 by mathmax by abdo last updated on 08/Jul/19
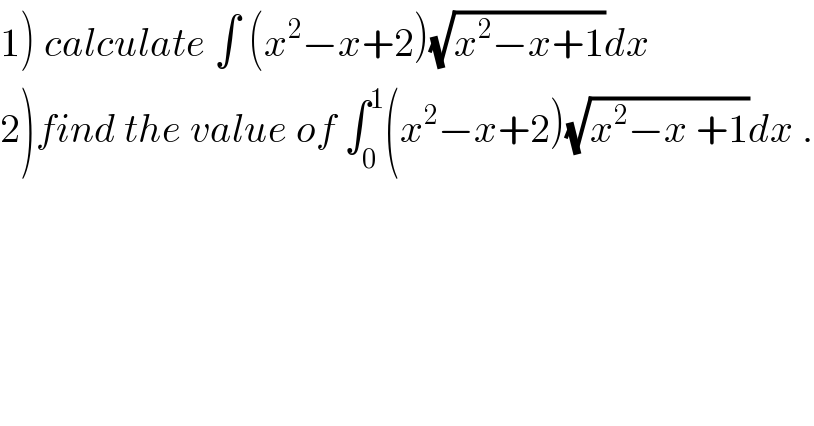
$$\left.\mathrm{1}\right)\:{calculate}\:\int\:\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx} \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}{dx}\:. \\ $$
Commented by Prithwish sen last updated on 08/Jul/19
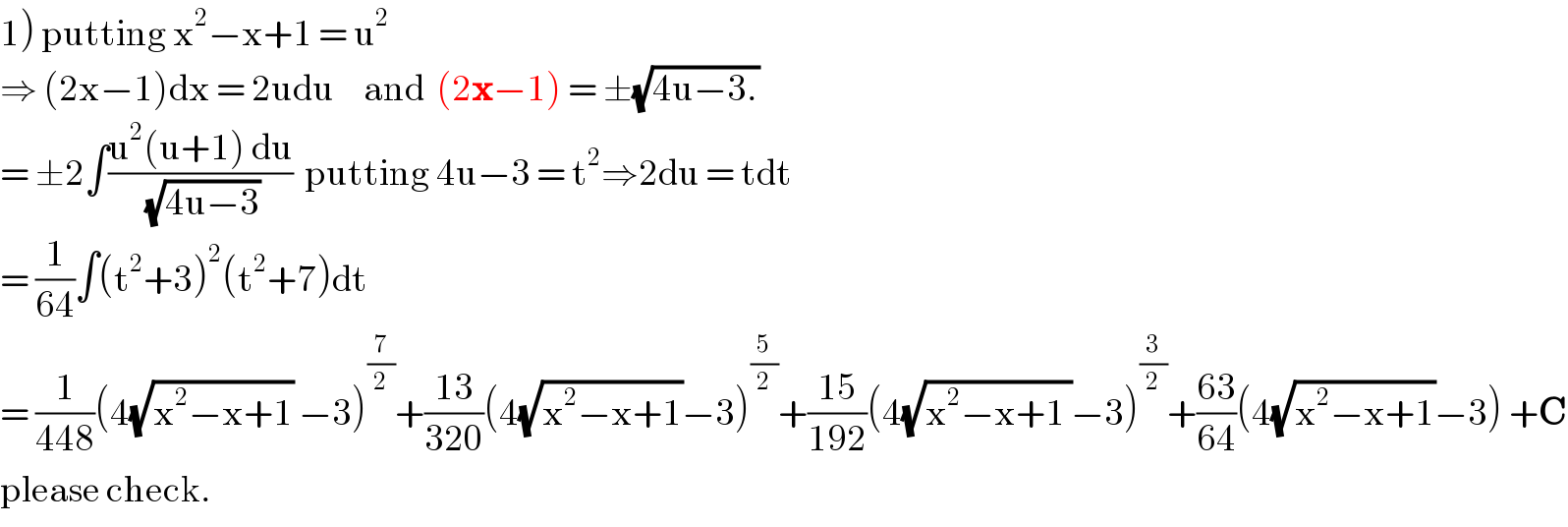
$$\left.\mathrm{1}\right)\:\mathrm{putting}\:\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\:=\:\mathrm{u}^{\mathrm{2}} \\ $$$$\Rightarrow\:\left(\mathrm{2x}−\mathrm{1}\right)\mathrm{dx}\:=\:\mathrm{2udu}\:\:\:\:\:\mathrm{and}\:\:\left(\mathrm{2}\boldsymbol{\mathrm{x}}−\mathrm{1}\right)\:=\:\pm\sqrt{\mathrm{4u}−\mathrm{3}.} \\ $$$$=\:\pm\mathrm{2}\int\frac{\mathrm{u}^{\mathrm{2}} \left(\mathrm{u}+\mathrm{1}\right)\:\mathrm{du}}{\sqrt{\mathrm{4u}−\mathrm{3}}}\:\:\mathrm{putting}\:\mathrm{4u}−\mathrm{3}\:=\:\mathrm{t}^{\mathrm{2}} \Rightarrow\mathrm{2du}\:=\:\mathrm{tdt} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{64}}\int\left(\mathrm{t}^{\mathrm{2}} +\mathrm{3}\right)^{\mathrm{2}} \left(\mathrm{t}^{\mathrm{2}} +\mathrm{7}\right)\mathrm{dt} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{448}}\left(\mathrm{4}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}\:−\mathrm{3}\right)^{\frac{\mathrm{7}}{\mathrm{2}}} +\frac{\mathrm{13}}{\mathrm{320}}\left(\mathrm{4}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}−\mathrm{3}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} +\frac{\mathrm{15}}{\mathrm{192}}\left(\mathrm{4}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\:}−\mathrm{3}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} +\frac{\mathrm{63}}{\mathrm{64}}\left(\mathrm{4}\sqrt{\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}}−\mathrm{3}\right)\:+\boldsymbol{\mathrm{C}} \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$
Commented by MJS last updated on 08/Jul/19

$$\mathrm{something}\:\mathrm{went}\:\mathrm{wrong} \\ $$$$\mathrm{you}\:\mathrm{can}\:\mathrm{put}\:{t}=\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:\rightarrow\:{dx}=\mathrm{2}{dt}\frac{\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}}{\mathrm{2}{x}−\mathrm{1}};\:{x}=\frac{\mathrm{1}+\sqrt{\mathrm{4}{t}^{\mathrm{2}} −\mathrm{3}}}{} \\ $$$$\Rightarrow\:\mathrm{2}\int\frac{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)}{\sqrt{\mathrm{4}{t}^{\mathrm{2}} −\mathrm{3}}} \\ $$$$\mathrm{or}\:\mathrm{you}\:\mathrm{can}\:\mathrm{put}\:{t}={x}^{\mathrm{2}} −{x}+\mathrm{1}\:\rightarrow\:{dx}=\frac{{dt}}{\mathrm{2}{x}−\mathrm{1}};\:{x}=\frac{\mathrm{1}+\sqrt{\mathrm{4}{u}−\mathrm{3}}}{\mathrm{2}} \\ $$$$\Rightarrow\:\int\frac{\sqrt{{t}}\left({t}+\mathrm{1}\right)}{\sqrt{\mathrm{4}{t}−\mathrm{3}}} \\ $$
Commented by Prithwish sen last updated on 08/Jul/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{will}\:\mathrm{check}\:\mathrm{it}. \\ $$
Commented by mathmax by abdo last updated on 08/Jul/19

$$\left.\mathrm{1}\right)\:{let}\:{I}\:=\int\:\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}\:{we}\:{have} \\ $$$${x}^{\mathrm{2}} −{x}\:+\mathrm{1}\:={x}^{\mathrm{2}} −\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}}{x}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}\:=\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}\:\:{so}\:{we}\:{use}\:{the} \\ $$$${changement}\:{x}−\frac{\mathrm{1}}{\mathrm{2}}\:=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)\:\Rightarrow \\ $$$$\Rightarrow\:{I}\:=\:\int\:\left(\:\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)\right)^{\mathrm{2}} −\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)\right)\:+\mathrm{2}\right)\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{ch}\left({t}\right){dt} \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\int\:\:\left\{\:\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{3}}{sh}\left({t}\right)\:+\mathrm{3}{sh}^{\mathrm{2}} \left({t}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)+\mathrm{2}−\frac{\mathrm{1}}{\mathrm{2}}\right){ch}\left({t}\right){dt}\right. \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\int\:\:\:\left\{\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)\:+\frac{\mathrm{3}}{\mathrm{4}}{sh}^{\mathrm{2}} \left({t}\right)−\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{sh}\left({t}\right)\:+\frac{\mathrm{7}}{\mathrm{4}}\right\}{ch}\left({t}\right){dt} \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{8}}\:\int\:{sh}\left({t}\right){ch}\left({t}\right){dt}\:+\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{8}}\:\int\:{ch}\left({t}\right){dt} \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{16}}{sh}^{\mathrm{2}} \left({t}\right)\:+\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{8}}\:{sh}\left({t}\right)\:+{c}\: \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{16}}\frac{{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{8}}{sh}\left({t}\right)\:+{c} \\ $$$$=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{32}}\left\{\:{ch}\left(\mathrm{2}{t}\right)−\mathrm{1}\right\}\:+\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{8}}{sh}\left({t}\right)\:+{c}\:. \\ $$$${we}\:{have}\:{t}\:={argsh}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\:={ln}\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right) \\ $$$${ch}\left(\mathrm{2}{t}\right)\:=\frac{{e}^{\mathrm{2}{t}} \:+{e}^{−\mathrm{2}{t}} }{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right)^{\mathrm{2}} +\frac{\mathrm{1}}{\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\left.\sqrt{\mathrm{3}}\right)}\right)^{\mathrm{2}} }\right.}\right\} \\ $$$$\left.{sh}\left({t}\right)\:=\frac{{e}^{{t}} −{e}^{−{t}} }{\mathrm{2}}\:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right.}\right)^{\mathrm{2}} −\:\frac{\mathrm{1}}{\left.\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\left(\frac{\mathrm{2}{x}−\mathrm{1}}{\sqrt{\mathrm{3}}}\right.}\right)^{\mathrm{2}} }\right\} \\ $$$${so}\:{the}\:{value}\:{of}\:{I}\:{is}\:{known}. \\ $$
Commented by mathmax by abdo last updated on 08/Jul/19
![2) ∫_0 ^1 (x^2 −x+2)(√(x^2 −x+1))dx =[F(x)]_0 ^1 =F(1)−F(0) F(1)=((3(√3))/(32)){(1/2)((1/(√3)) +(√(1+(1/3))))^2 +(1/(((1/(√3))+(√(1+(1/3))))^2 ))}−1} +((7(√3))/(16)){ (1/(√3)) +(√(1+(1/3))) −(1/((1/(√3))+(√(1+(1/3)))))} F(0) =((3(√3))/(32)){(−(1/3) +(√(1+(1/3))))^2 +(1/((−(1/3) +(√(1+(1/3))))^2 ))} +((7(√3))/(16)){−(1/(√3)) +(√(1+(1/3)))−(1/(−(1/(√3))+(√(1+(1/3)))))}](Q63773.png)
$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}\:=\left[{F}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} ={F}\left(\mathrm{1}\right)−{F}\left(\mathrm{0}\right) \\ $$$$\left.{F}\left(\mathrm{1}\right)=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{32}}\left\{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}\right)^{\mathrm{2}} \:\:+\frac{\mathrm{1}}{\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}\right)^{\mathrm{2}} }\right\}−\mathrm{1}\right\} \\ $$$$+\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{16}}\left\{\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}\:−\frac{\mathrm{1}}{\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}}\right\} \\ $$$${F}\left(\mathrm{0}\right)\:=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{32}}\left\{\left(−\frac{\mathrm{1}}{\mathrm{3}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\left(−\frac{\mathrm{1}}{\mathrm{3}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}\right)^{\mathrm{2}} }\right\} \\ $$$$+\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{16}}\left\{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}−\frac{\mathrm{1}}{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}+\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}}\right\} \\ $$
Commented by mathmax by abdo last updated on 08/Jul/19
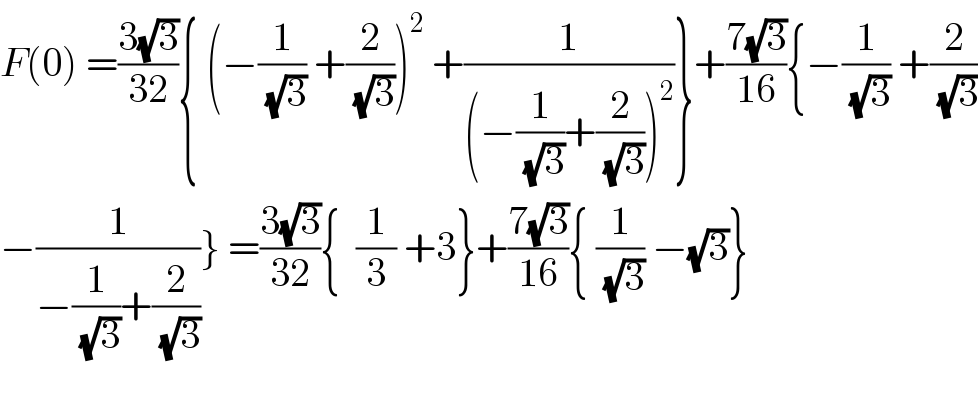
$${F}\left(\mathrm{0}\right)\:=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{32}}\left\{\:\left(−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} \:+\frac{\mathrm{1}}{\left(−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}+\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} }\right\}+\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{16}}\left\{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:+\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\right. \\ $$$$\left.−\frac{\mathrm{1}}{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}+\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}}\right\}\:=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{32}}\left\{\:\:\frac{\mathrm{1}}{\mathrm{3}}\:+\mathrm{3}\right\}+\frac{\mathrm{7}\sqrt{\mathrm{3}}}{\mathrm{16}}\left\{\:\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\:−\sqrt{\mathrm{3}}\right\} \\ $$$$ \\ $$
Answered by MJS last updated on 08/Jul/19
![∫(x^2 −x+2)(√(x^2 −x+1))dx= [t=sinh^(−1) (((√3)(2x−1))/3) → dx=(√(x^2 −x+1))dt] =((75)/(128))∫dt+(9/(128))∫cosh 4t dt+((21)/(32))∫cosh 2t dt= =((75)/(128))t+(9/(512))sinh 4t +((21)/(64))sinh 2t= =((75)/(128))sinh^(−1) (((√3)(2x−1))/3) +(1/(64))(2x−1)(8x^2 −8x+5)(√(x^2 −x+1)) +(7/(16))(2x−1)(√(x^2 −x+1))= =((75)/(128))sinh^(−1) (((√3)(2x−1))/3) +(1/(64))(2x−1)(8x^2 −8x+33)(√(x^2 −x+1)) +C ∫_0 ^1 (x^2 −x+2)(√(x^2 −x+1))dx=((33)/(32))+((75)/(64))sinh^(−1) ((√3)/3) =((33)/(32))+((75)/(128))ln 3](Q63737.png)
$$\int\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{sinh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{3}}\:\rightarrow\:{dx}=\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dt}\right] \\ $$$$=\frac{\mathrm{75}}{\mathrm{128}}\int{dt}+\frac{\mathrm{9}}{\mathrm{128}}\int\mathrm{cosh}\:\mathrm{4}{t}\:{dt}+\frac{\mathrm{21}}{\mathrm{32}}\int\mathrm{cosh}\:\mathrm{2}{t}\:{dt}= \\ $$$$=\frac{\mathrm{75}}{\mathrm{128}}{t}+\frac{\mathrm{9}}{\mathrm{512}}\mathrm{sinh}\:\mathrm{4}{t}\:+\frac{\mathrm{21}}{\mathrm{64}}\mathrm{sinh}\:\mathrm{2}{t}= \\ $$$$=\frac{\mathrm{75}}{\mathrm{128}}\mathrm{sinh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{64}}\left(\mathrm{2}{x}−\mathrm{1}\right)\left(\mathrm{8}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{5}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:+\frac{\mathrm{7}}{\mathrm{16}}\left(\mathrm{2}{x}−\mathrm{1}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}= \\ $$$$=\frac{\mathrm{75}}{\mathrm{128}}\mathrm{sinh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{3}}\left(\mathrm{2}{x}−\mathrm{1}\right)}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{64}}\left(\mathrm{2}{x}−\mathrm{1}\right)\left(\mathrm{8}{x}^{\mathrm{2}} −\mathrm{8}{x}+\mathrm{33}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:+{C} \\ $$$$ \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left({x}^{\mathrm{2}} −{x}+\mathrm{2}\right)\sqrt{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}=\frac{\mathrm{33}}{\mathrm{32}}+\frac{\mathrm{75}}{\mathrm{64}}\mathrm{sinh}^{−\mathrm{1}} \:\frac{\sqrt{\mathrm{3}}}{\mathrm{3}}\:=\frac{\mathrm{33}}{\mathrm{32}}+\frac{\mathrm{75}}{\mathrm{128}}\mathrm{ln}\:\mathrm{3} \\ $$
Commented by Prithwish sen last updated on 08/Jul/19
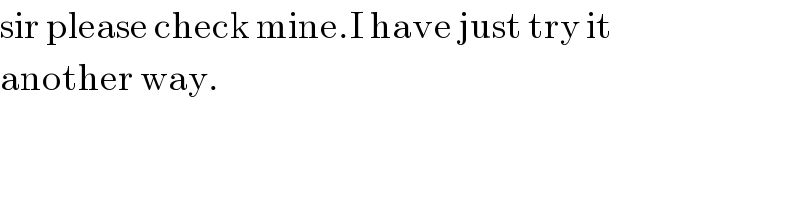
$$\mathrm{sir}\:\mathrm{please}\:\mathrm{check}\:\mathrm{mine}.\mathrm{I}\:\mathrm{have}\:\mathrm{just}\:\mathrm{try}\:\mathrm{it}\: \\ $$$$\mathrm{another}\:\mathrm{way}. \\ $$
Commented by mathmax by abdo last updated on 08/Jul/19
$${thank}\:{you}\:{sir}\:{mjs}. \\ $$
