
Question Number 63517 by Rio Michael last updated on 05/Jul/19

$$\mathrm{Given}\:\mathrm{that}\:\:\mid{z}−\mathrm{6}\mid=\mathrm{2}\mid{z}+\mathrm{6}−\mathrm{9}{i}\mid, \\ $$$$\left.\mathrm{a}\right)\:\mathrm{Use}\:\mathrm{algebra}\:\mathrm{to}\:\mathrm{show}\:\mathrm{that}\:\mathrm{the}\:\mathrm{locus}\:\mathrm{of}\:{z}\:\mathrm{is}\:\mathrm{a}\:\mathrm{circle}, \\ $$$$\mathrm{stating}\:\mathrm{its}\:\mathrm{center}\:\mathrm{and}\:\mathrm{its}\:\mathrm{radius}. \\ $$$$\left.\mathrm{b}\right)\:\mathrm{sketch}\:\mathrm{the}\:\mathrm{locus}\:{z}\:\mathrm{on}\:\mathrm{an}\:\mathrm{argand}\:\mathrm{diagram}. \\ $$
Answered by MJS last updated on 05/Jul/19
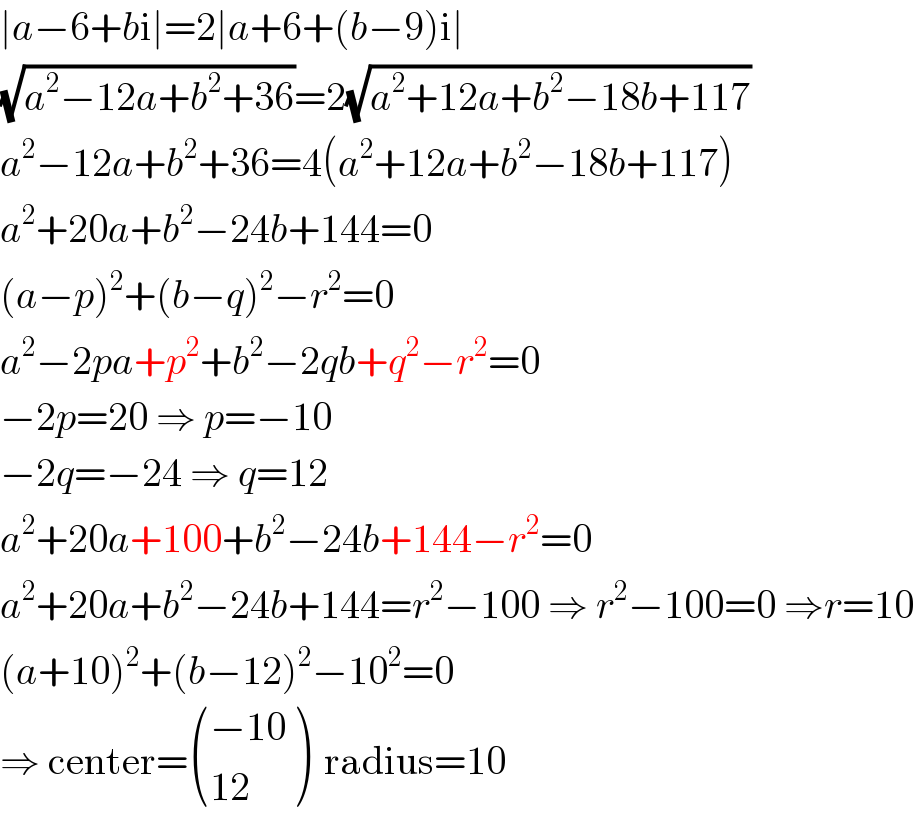
$$\mid{a}−\mathrm{6}+{b}\mathrm{i}\mid=\mathrm{2}\mid{a}+\mathrm{6}+\left({b}−\mathrm{9}\right)\mathrm{i}\mid \\ $$$$\sqrt{{a}^{\mathrm{2}} −\mathrm{12}{a}+{b}^{\mathrm{2}} +\mathrm{36}}=\mathrm{2}\sqrt{{a}^{\mathrm{2}} +\mathrm{12}{a}+{b}^{\mathrm{2}} −\mathrm{18}{b}+\mathrm{117}} \\ $$$${a}^{\mathrm{2}} −\mathrm{12}{a}+{b}^{\mathrm{2}} +\mathrm{36}=\mathrm{4}\left({a}^{\mathrm{2}} +\mathrm{12}{a}+{b}^{\mathrm{2}} −\mathrm{18}{b}+\mathrm{117}\right) \\ $$$${a}^{\mathrm{2}} +\mathrm{20}{a}+{b}^{\mathrm{2}} −\mathrm{24}{b}+\mathrm{144}=\mathrm{0} \\ $$$$\left({a}−{p}\right)^{\mathrm{2}} +\left({b}−{q}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}^{\mathrm{2}} −\mathrm{2}{pa}+{p}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{qb}+{q}^{\mathrm{2}} −{r}^{\mathrm{2}} =\mathrm{0} \\ $$$$−\mathrm{2}{p}=\mathrm{20}\:\Rightarrow\:{p}=−\mathrm{10} \\ $$$$−\mathrm{2}{q}=−\mathrm{24}\:\Rightarrow\:{q}=\mathrm{12} \\ $$$${a}^{\mathrm{2}} +\mathrm{20}{a}+\mathrm{100}+{b}^{\mathrm{2}} −\mathrm{24}{b}+\mathrm{144}−{r}^{\mathrm{2}} =\mathrm{0} \\ $$$${a}^{\mathrm{2}} +\mathrm{20}{a}+{b}^{\mathrm{2}} −\mathrm{24}{b}+\mathrm{144}={r}^{\mathrm{2}} −\mathrm{100}\:\Rightarrow\:{r}^{\mathrm{2}} −\mathrm{100}=\mathrm{0}\:\Rightarrow{r}=\mathrm{10} \\ $$$$\left({a}+\mathrm{10}\right)^{\mathrm{2}} +\left({b}−\mathrm{12}\right)^{\mathrm{2}} −\mathrm{10}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{center}=\begin{pmatrix}{−\mathrm{10}}\\{\mathrm{12}}\end{pmatrix}\:\:\mathrm{radius}=\mathrm{10} \\ $$
Commented by Rio Michael last updated on 05/Jul/19

$${correct}! \\ $$
