
Question Number 63481 by naka3546 last updated on 04/Jul/19
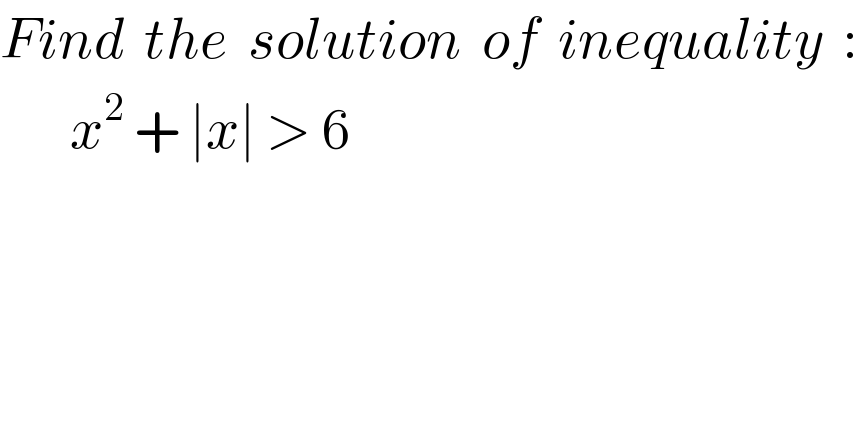
$${Find}\:\:{the}\:\:{solution}\:\:{of}\:\:{inequality}\:\:: \\ $$ $$\:\:\:\:\:\:\:{x}^{\mathrm{2}} \:+\:\mid{x}\mid\:>\:\mathrm{6} \\ $$
Commented bymathmax by abdo last updated on 04/Jul/19
![(ine) ⇒∣x∣^2 +∣x∣−6>0 ⇒t^2 +t−6>0 Δ=1−4(−6)=25 ⇒ t_1 =((−1+5)/2) =2 and t_2 =((−1−5)/2) =−3 ⇒ ∣x∣^2 +∣x∣−6 =(∣x∣−2)(∣x∣+3) so (ine) ⇒{∣x∣−2}{∣x∣+3}>0 ⇒ ∣x∣−2 >0 (because ∣x∣ +3>0 ⇒ x>2 or x<−2 ⇒ x ∈]−∞,−2[∪]2,+∞[](Q63496.png)
$$\left({ine}\right)\:\Rightarrow\mid{x}\mid^{\mathrm{2}} +\mid{x}\mid−\mathrm{6}>\mathrm{0}\:\Rightarrow{t}^{\mathrm{2}} +{t}−\mathrm{6}>\mathrm{0} \\ $$ $$\Delta=\mathrm{1}−\mathrm{4}\left(−\mathrm{6}\right)=\mathrm{25}\:\Rightarrow\:{t}_{\mathrm{1}} =\frac{−\mathrm{1}+\mathrm{5}}{\mathrm{2}}\:=\mathrm{2}\:\:{and}\:{t}_{\mathrm{2}} =\frac{−\mathrm{1}−\mathrm{5}}{\mathrm{2}}\:=−\mathrm{3}\:\Rightarrow \\ $$ $$\mid{x}\mid^{\mathrm{2}} +\mid{x}\mid−\mathrm{6}\:=\left(\mid{x}\mid−\mathrm{2}\right)\left(\mid{x}\mid+\mathrm{3}\right)\:\:\:{so}\:\:\left({ine}\right)\:\Rightarrow\left\{\mid{x}\mid−\mathrm{2}\right\}\left\{\mid{x}\mid+\mathrm{3}\right\}>\mathrm{0}\:\Rightarrow \\ $$ $$\mid{x}\mid−\mathrm{2}\:>\mathrm{0}\:\:\:\left({because}\:\mid{x}\mid\:+\mathrm{3}>\mathrm{0}\:\Rightarrow\:{x}>\mathrm{2}\:{or}\:{x}<−\mathrm{2}\:\Rightarrow\right. \\ $$ $$\left.{x}\:\in\right]−\infty,−\mathrm{2}\left[\cup\right]\mathrm{2},+\infty\left[\right. \\ $$ $$ \\ $$
Answered by MJS last updated on 04/Jul/19
![x>0 x^2 +x>6 x^2 +x−6=0 ⇒ x=−3∨x=2 ⇒ x<−3∨x>2 but x>0 ⇒ x>2 x<0 x^2 −x>6 x^2 −x−6=0 ⇒ x=−2∨x=3 ⇒ x<−2∨x>3 but x<0 ⇒ x<−2 x^2 +∣x∣>6 ⇒ x<−2∨2<x ⇔ x∈]−∞; −2[∪]2; +∞[](Q63501.png)
$${x}>\mathrm{0} \\ $$ $${x}^{\mathrm{2}} +{x}>\mathrm{6} \\ $$ $${x}^{\mathrm{2}} +{x}−\mathrm{6}=\mathrm{0}\:\Rightarrow\:{x}=−\mathrm{3}\vee{x}=\mathrm{2} \\ $$ $$\Rightarrow\:{x}<−\mathrm{3}\vee{x}>\mathrm{2}\:\mathrm{but}\:{x}>\mathrm{0} \\ $$ $$\Rightarrow\:{x}>\mathrm{2} \\ $$ $$ \\ $$ $${x}<\mathrm{0} \\ $$ $${x}^{\mathrm{2}} −{x}>\mathrm{6} \\ $$ $${x}^{\mathrm{2}} −{x}−\mathrm{6}=\mathrm{0}\:\Rightarrow\:{x}=−\mathrm{2}\vee{x}=\mathrm{3} \\ $$ $$\Rightarrow\:{x}<−\mathrm{2}\vee{x}>\mathrm{3}\:\mathrm{but}\:{x}<\mathrm{0} \\ $$ $$\Rightarrow\:{x}<−\mathrm{2} \\ $$ $$ \\ $$ $$\left.{x}^{\mathrm{2}} +\mid{x}\mid>\mathrm{6}\:\Rightarrow\:{x}<−\mathrm{2}\vee\mathrm{2}<{x}\:\Leftrightarrow\:{x}\in\right]−\infty;\:−\mathrm{2}\left[\cup\right]\mathrm{2};\:+\infty\left[\right. \\ $$
