
Question Number 63457 by smartsmith459@gmail.com last updated on 04/Jul/19
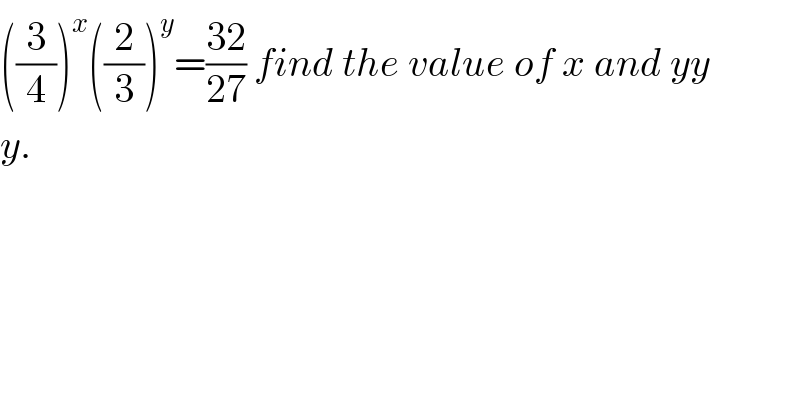
$$\left(\frac{\mathrm{3}}{\mathrm{4}}\right)^{{x}} \left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{{y}} =\frac{\mathrm{32}}{\mathrm{27}}\:{find}\:{the}\:{value}\:{of}\:{x}\:{and}\:{yy} \\ $$$${y}. \\ $$
Commented by Prithwish sen last updated on 04/Jul/19
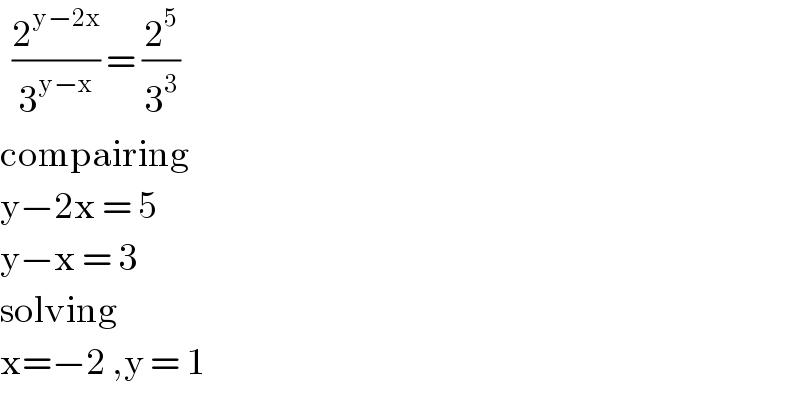
$$\:\:\frac{\mathrm{2}^{\mathrm{y}−\mathrm{2x}} }{\mathrm{3}^{\mathrm{y}−\mathrm{x}} }\:=\:\frac{\mathrm{2}^{\mathrm{5}} }{\mathrm{3}^{\mathrm{3}} } \\ $$$$\mathrm{compairing} \\ $$$$\mathrm{y}−\mathrm{2x}\:=\:\mathrm{5} \\ $$$$\mathrm{y}−\mathrm{x}\:=\:\mathrm{3} \\ $$$$\mathrm{solving} \\ $$$$\mathrm{x}=−\mathrm{2}\:,\mathrm{y}\:=\:\mathrm{1} \\ $$
Answered by Joel122 last updated on 04/Jul/19
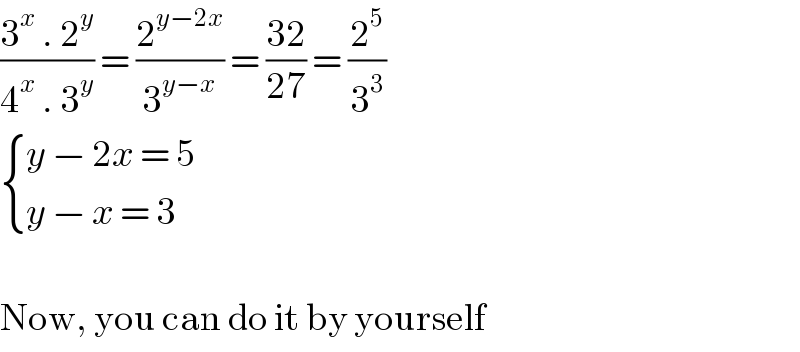
$$\frac{\mathrm{3}^{{x}} \:.\:\mathrm{2}^{{y}} }{\mathrm{4}^{{x}} \:.\:\mathrm{3}^{{y}} }\:=\:\frac{\mathrm{2}^{{y}−\mathrm{2}{x}} }{\mathrm{3}^{{y}−{x}} }\:=\:\frac{\mathrm{32}}{\mathrm{27}}\:=\:\frac{\mathrm{2}^{\mathrm{5}} }{\mathrm{3}^{\mathrm{3}} } \\ $$$$\begin{cases}{{y}\:−\:\mathrm{2}{x}\:=\:\mathrm{5}}\\{{y}\:−\:{x}\:=\:\mathrm{3}}\end{cases} \\ $$$$ \\ $$$$\mathrm{Now},\:\mathrm{you}\:\mathrm{can}\:\mathrm{do}\:\mathrm{it}\:\mathrm{by}\:\mathrm{yourself} \\ $$
