
Question Number 63447 by minh2001 last updated on 04/Jul/19

$${How}\:{to}\:{calculate}\:\lceil\left({n}\right)\: \\ $$$${using}\:{gamma}\:{function} \\ $$$$\forall{n}\in{R} \\ $$
Commented by minh2001 last updated on 04/Jul/19
$${I}\:{can}'{t}\:{remember}\:{it}\:{until}\: \\ $$$${now} \\ $$
Commented by mathmax by abdo last updated on 04/Jul/19
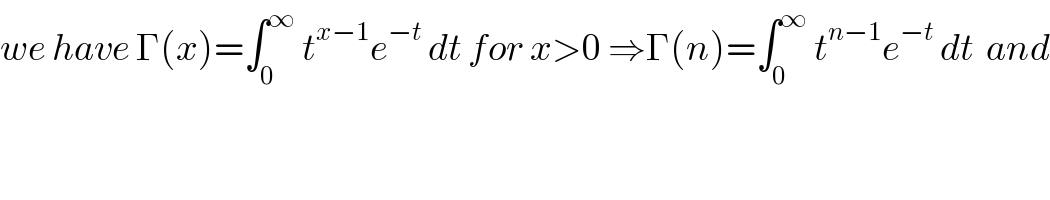
$${we}\:{have}\:\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} {e}^{−{t}} \:{dt}\:{for}\:{x}>\mathrm{0}\:\Rightarrow\Gamma\left({n}\right)=\int_{\mathrm{0}} ^{\infty} \:{t}^{{n}−\mathrm{1}} {e}^{−{t}} \:{dt}\:\:{and} \\ $$
Answered by MJS last updated on 04/Jul/19
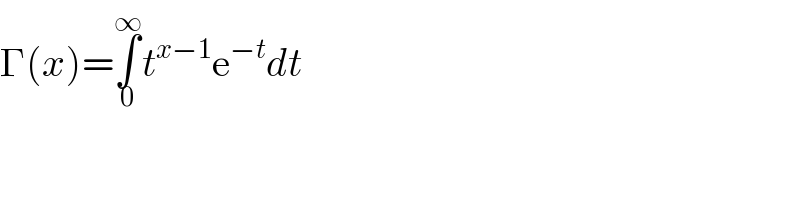
$$\Gamma\left({x}\right)=\underset{\mathrm{0}} {\overset{\infty} {\int}}{t}^{{x}−\mathrm{1}} \mathrm{e}^{−{t}} {dt} \\ $$
