
Question Number 63404 by mathmax by abdo last updated on 03/Jul/19
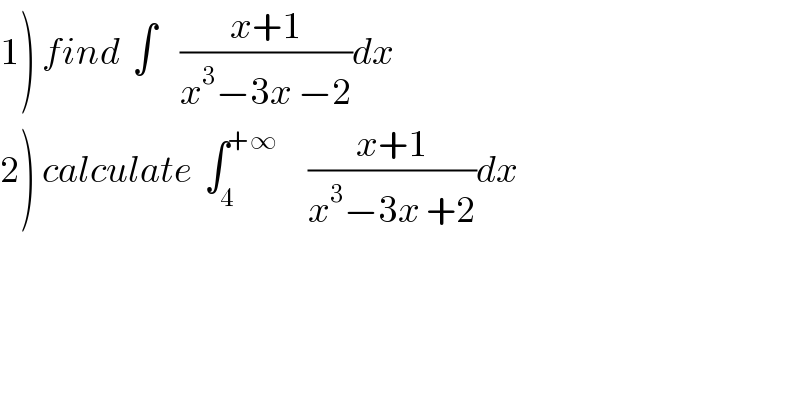
$$\left.\mathrm{1}\right)\:{find}\:\:\int\:\:\:\:\frac{{x}+\mathrm{1}}{{x}^{\mathrm{3}} −\mathrm{3}{x}\:−\mathrm{2}}{dx} \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\:\int_{\mathrm{4}} ^{+\infty} \:\:\:\:\:\frac{{x}+\mathrm{1}}{{x}^{\mathrm{3}} −\mathrm{3}{x}\:+\mathrm{2}}{dx} \\ $$
Commented by MJS last updated on 03/Jul/19

$$\left.−\:\mathrm{in}\:\mathrm{1}\right) \\ $$$$\left.+\:\mathrm{in}\:\mathrm{2}\right) \\ $$$$\mathrm{is}\:\mathrm{this}\:\mathrm{right}? \\ $$
Commented by mathmax by abdo last updated on 03/Jul/19
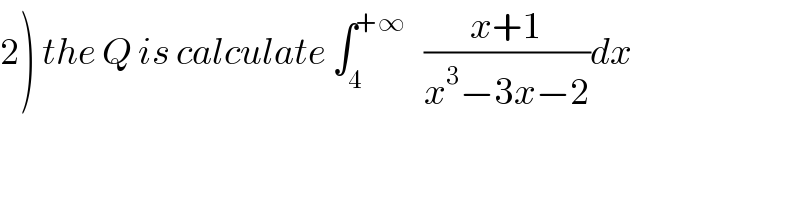
$$\left.\mathrm{2}\right)\:{the}\:{Q}\:{is}\:{calculate}\:\int_{\mathrm{4}} ^{+\infty} \:\:\:\frac{{x}+\mathrm{1}}{{x}^{\mathrm{3}} −\mathrm{3}{x}−\mathrm{2}}{dx}\: \\ $$
Answered by MJS last updated on 03/Jul/19
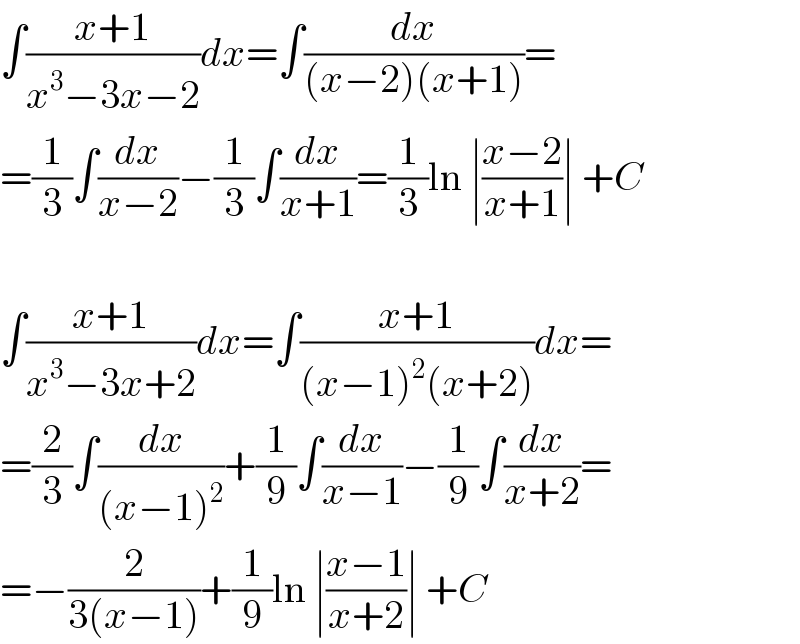
$$\int\frac{{x}+\mathrm{1}}{{x}^{\mathrm{3}} −\mathrm{3}{x}−\mathrm{2}}{dx}=\int\frac{{dx}}{\left({x}−\mathrm{2}\right)\left({x}+\mathrm{1}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}−\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{{x}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{2}}{{x}+\mathrm{1}}\mid\:+{C} \\ $$$$ \\ $$$$\int\frac{{x}+\mathrm{1}}{{x}^{\mathrm{3}} −\mathrm{3}{x}+\mathrm{2}}{dx}=\int\frac{{x}+\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{2}\right)}{dx}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{9}}\int\frac{{dx}}{{x}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{9}}\int\frac{{dx}}{{x}+\mathrm{2}}= \\ $$$$=−\frac{\mathrm{2}}{\mathrm{3}\left({x}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{9}}\mathrm{ln}\:\mid\frac{{x}−\mathrm{1}}{{x}+\mathrm{2}}\mid\:+{C} \\ $$
Commented by mathmax by abdo last updated on 03/Jul/19

$${thank}\:{you}\:{sir}. \\ $$
