
Question Number 63361 by rajesh4661kumar@gamil.com last updated on 03/Jul/19
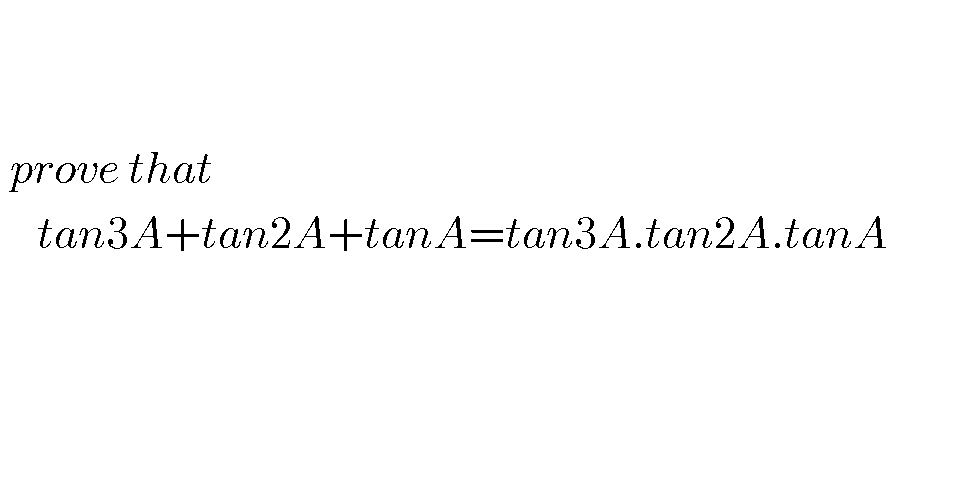
Commented by Prithwish sen last updated on 03/Jul/19
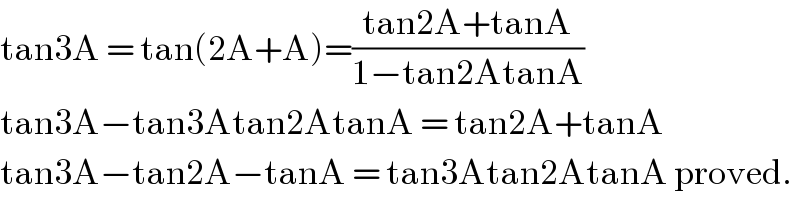
$$\mathrm{tan3A}\:=\:\mathrm{tan}\left(\mathrm{2A}+\mathrm{A}\right)=\frac{\mathrm{tan2A}+\mathrm{tanA}}{\mathrm{1}−\mathrm{tan2AtanA}} \\ $$$$\mathrm{tan3A}−\mathrm{tan3Atan2AtanA}\:=\:\mathrm{tan2A}+\mathrm{tanA} \\ $$$$\mathrm{tan3A}−\mathrm{tan2A}−\mathrm{tanA}\:=\:\mathrm{tan3Atan2AtanA}\:\mathrm{proved}. \\ $$
Commented by Hope last updated on 03/Jul/19
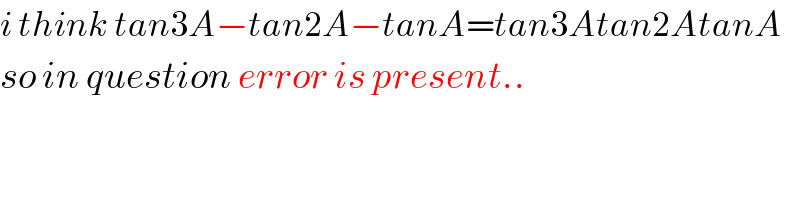
$${i}\:{think}\:{tan}\mathrm{3}{A}−{tan}\mathrm{2}{A}−{tanA}={tan}\mathrm{3}{Atan}\mathrm{2}{AtanA} \\ $$$${so}\:{in}\:{question}\:{error}\:{is}\:{present}.. \\ $$
Commented by Prithwish sen last updated on 03/Jul/19

$$\mathrm{yes}\:\mathrm{your}\:\mathrm{are}\:\mathrm{right}.\: \\ $$
