
Question Number 63301 by Rio Michael last updated on 02/Jul/19
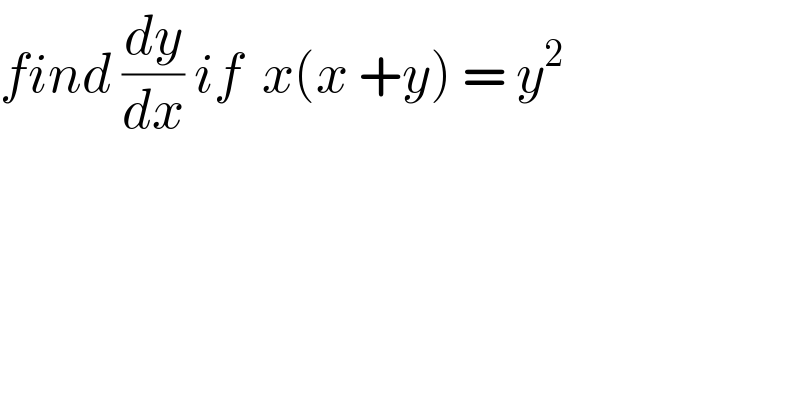
$${find}\:\frac{{dy}}{{dx}}\:{if}\:\:{x}\left({x}\:+{y}\right)\:=\:{y}^{\mathrm{2}} \\ $$
Commented by kaivan.ahmadi last updated on 02/Jul/19
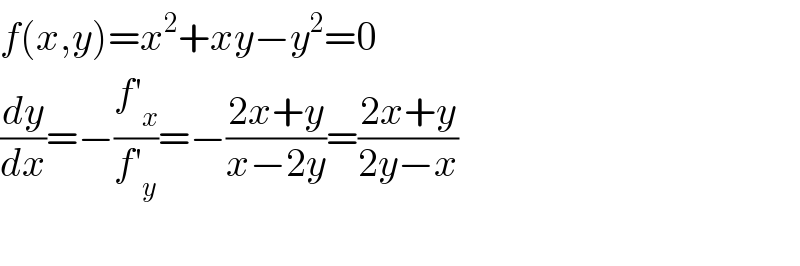
$${f}\left({x},{y}\right)={x}^{\mathrm{2}} +{xy}−{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\frac{{dy}}{{dx}}=−\frac{{f}'_{{x}} }{{f}'_{{y}} }=−\frac{\mathrm{2}{x}+{y}}{{x}−\mathrm{2}{y}}=\frac{\mathrm{2}{x}+{y}}{\mathrm{2}{y}−{x}} \\ $$$$ \\ $$
Commented by Rio Michael last updated on 02/Jul/19
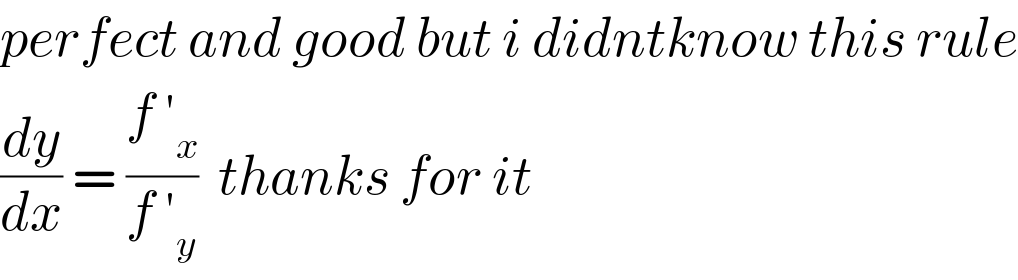
$${perfect}\:{and}\:{good}\:{but}\:{i}\:{didntknow}\:{this}\:{rule} \\ $$$$\frac{{dy}}{{dx}}\:=\:\frac{{f}\:'_{{x}} }{{f}\:'_{{y}} }\:\:{thanks}\:{for}\:{it} \\ $$
Commented by Prithwish sen last updated on 02/Jul/19
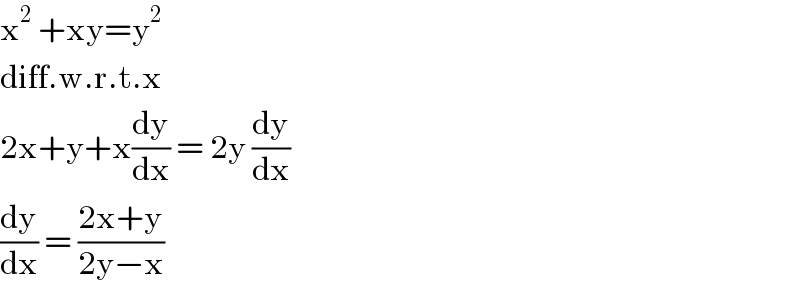
$$\mathrm{x}^{\mathrm{2}} \:+\mathrm{xy}=\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{diff}.\mathrm{w}.\mathrm{r}.\mathrm{t}.\mathrm{x} \\ $$$$\mathrm{2x}+\mathrm{y}+\mathrm{x}\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\mathrm{2y}\:\frac{\mathrm{dy}}{\mathrm{dx}} \\ $$$$\frac{\mathrm{dy}}{\mathrm{dx}}\:=\:\frac{\mathrm{2x}+\mathrm{y}}{\mathrm{2y}−\mathrm{x}} \\ $$
Commented by Rio Michael last updated on 02/Jul/19
$${yes}\:{thats}\:{our}\:{style}..{do}\:{u}\:{offer}\:{mathematics}\:{mechanics} \\ $$
Commented by MJS last updated on 02/Jul/19

$$\mathrm{the}\:``\mathrm{long}\:\mathrm{version}'' \\ $$$${x}^{\mathrm{2}} +{xy}−{y}^{\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{differentiate}\:\mathrm{each}\:\mathrm{term}\:\mathrm{and}\:\mathrm{multiply}\:\mathrm{with} \\ $$$${dx}\:\mathrm{or}\:{dy}: \\ $$$${x}^{\mathrm{2}} \:\rightarrow\:\mathrm{2}{xdx} \\ $$$${xy}\:\rightarrow\:{ydx}+{xdy} \\ $$$${y}^{\mathrm{2}} \:\rightarrow\:\mathrm{2}{ydy} \\ $$$$\mathrm{2}{xdx}+{ydx}+{xdy}−\mathrm{2}{ydy}=\mathrm{0} \\ $$$$\mathrm{now}\:``\mathrm{split}''\:{dx}\:\mathrm{from}\:{dy} \\ $$$$\left(\mathrm{2}{x}+{y}\right){dx}=\left(\mathrm{2}{y}−{x}\right){dy} \\ $$$$\Rightarrow\:\frac{{dy}}{{dx}}=\frac{\mathrm{2}{x}+{y}}{\mathrm{2}{y}−{x}} \\ $$
Commented by Rio Michael last updated on 02/Jul/19
$${thats}\:{still}\:{good} \\ $$
Commented by mathmax by abdo last updated on 02/Jul/19
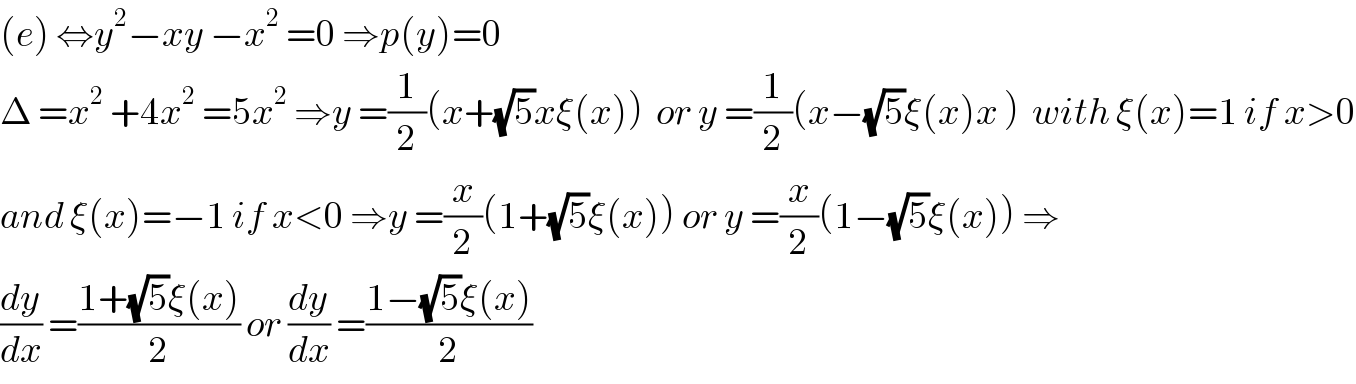
$$\left({e}\right)\:\Leftrightarrow{y}^{\mathrm{2}} −{xy}\:−{x}^{\mathrm{2}} \:=\mathrm{0}\:\Rightarrow{p}\left({y}\right)=\mathrm{0}\: \\ $$$$\Delta\:={x}^{\mathrm{2}} \:+\mathrm{4}{x}^{\mathrm{2}} \:=\mathrm{5}{x}^{\mathrm{2}} \:\Rightarrow{y}\:=\frac{\mathrm{1}}{\mathrm{2}}\left({x}+\sqrt{\mathrm{5}}{x}\xi\left({x}\right)\right)\:\:{or}\:{y}\:=\frac{\mathrm{1}}{\mathrm{2}}\left({x}−\sqrt{\mathrm{5}}\xi\left({x}\right){x}\:\right)\:\:{with}\:\xi\left({x}\right)=\mathrm{1}\:{if}\:{x}>\mathrm{0} \\ $$$${and}\:\xi\left({x}\right)=−\mathrm{1}\:{if}\:{x}<\mathrm{0}\:\Rightarrow{y}\:=\frac{{x}}{\mathrm{2}}\left(\mathrm{1}+\sqrt{\mathrm{5}}\xi\left({x}\right)\right)\:{or}\:{y}\:=\frac{{x}}{\mathrm{2}}\left(\mathrm{1}−\sqrt{\mathrm{5}}\xi\left({x}\right)\right)\:\Rightarrow \\ $$$$\frac{{dy}}{{dx}}\:=\frac{\mathrm{1}+\sqrt{\mathrm{5}}\xi\left({x}\right)}{\mathrm{2}}\:{or}\:\frac{{dy}}{{dx}}\:=\frac{\mathrm{1}−\sqrt{\mathrm{5}}\xi\left({x}\right)}{\mathrm{2}} \\ $$
Commented by ajfour last updated on 02/Jul/19

$${whats}\:\xi\:,\:{please}\:{lecture}\:{elaboratey}, \\ $$$${Sir}. \\ $$
Commented by mathmax by abdo last updated on 02/Jul/19
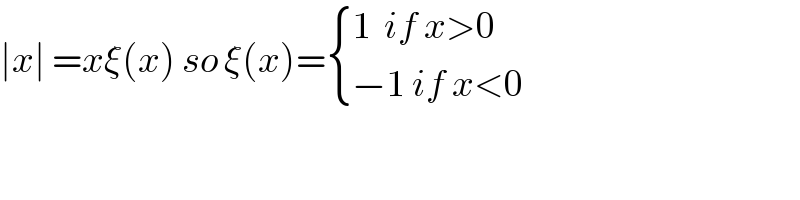
$$\mid{x}\mid\:={x}\xi\left({x}\right)\:{so}\:\xi\left({x}\right)=\begin{cases}{\mathrm{1}\:\:{if}\:{x}>\mathrm{0}}\\{−\mathrm{1}\:{if}\:{x}<\mathrm{0}}\end{cases} \\ $$
Answered by Smail last updated on 02/Jul/19
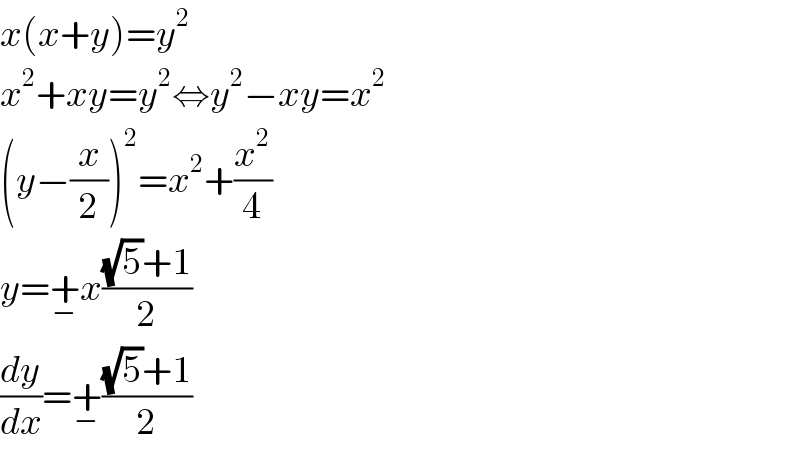
$${x}\left({x}+{y}\right)={y}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} +{xy}={y}^{\mathrm{2}} \Leftrightarrow{y}^{\mathrm{2}} −{xy}={x}^{\mathrm{2}} \\ $$$$\left({y}−\frac{{x}}{\mathrm{2}}\right)^{\mathrm{2}} ={x}^{\mathrm{2}} +\frac{{x}^{\mathrm{2}} }{\mathrm{4}} \\ $$$${y}=\underset{−} {+}{x}\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{dy}}{{dx}}=\underset{−} {+}\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Prithwish sen last updated on 02/Jul/19
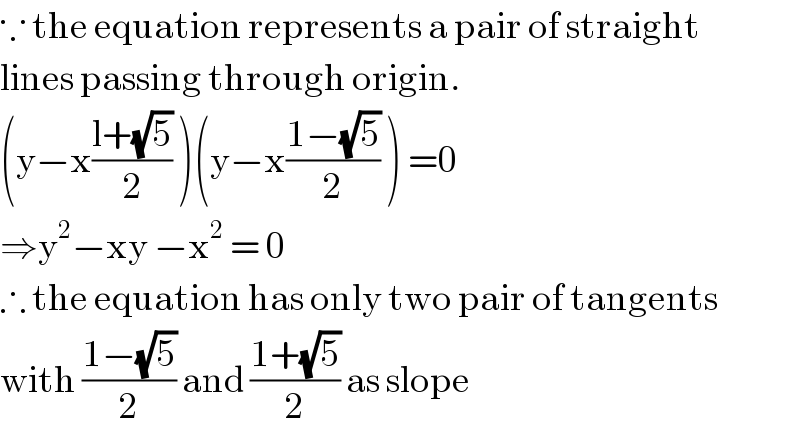
$$\because\:\mathrm{the}\:\mathrm{equation}\:\mathrm{represents}\:\mathrm{a}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{straight} \\ $$$$\mathrm{lines}\:\mathrm{passing}\:\mathrm{through}\:\mathrm{origin}. \\ $$$$\left(\mathrm{y}−\mathrm{x}\frac{\mathrm{l}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\right)\left(\mathrm{y}−\mathrm{x}\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:\right)\:=\mathrm{0} \\ $$$$\Rightarrow\mathrm{y}^{\mathrm{2}} −\mathrm{xy}\:−\mathrm{x}^{\mathrm{2}} \:=\:\mathrm{0} \\ $$$$\therefore\:\mathrm{the}\:\mathrm{equation}\:\mathrm{has}\:\mathrm{only}\:\mathrm{two}\:\mathrm{pair}\:\mathrm{of}\:\mathrm{tangents} \\ $$$$\mathrm{with}\:\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{and}\:\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:\mathrm{as}\:\mathrm{slope} \\ $$
Commented by Rio Michael last updated on 02/Jul/19
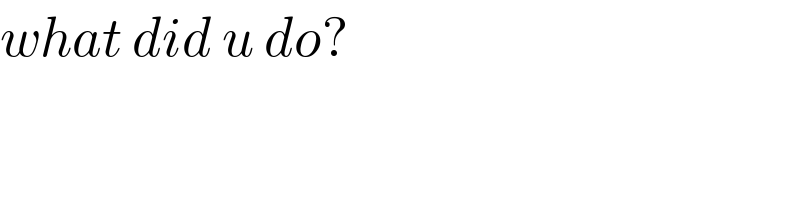
$${what}\:{did}\:{u}\:{do}? \\ $$
Commented by Smail last updated on 02/Jul/19
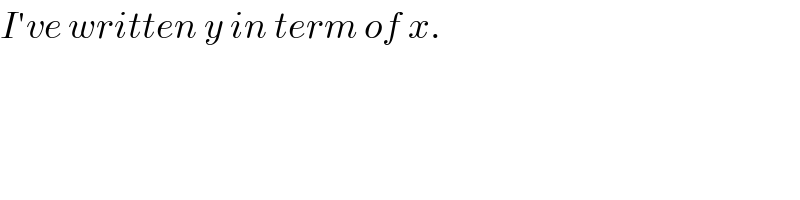
$${I}'{ve}\:{written}\:{y}\:{in}\:{term}\:{of}\:{x}. \\ $$
Commented by Rio Michael last updated on 02/Jul/19
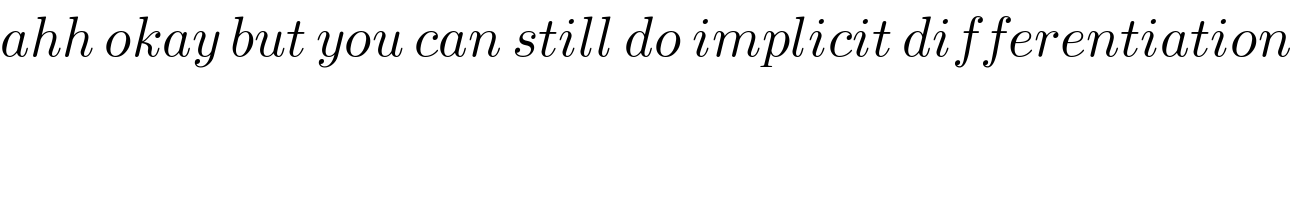
$${ahh}\:{okay}\:{but}\:{you}\:{can}\:{still}\:{do}\:{implicit}\:{differentiation} \\ $$
