
Question Number 63178 by ajfour last updated on 30/Jun/19
Commented by Prithwish sen last updated on 30/Jun/19
![Sir, whether the answer is [(((a+b)/2)),(((a+b)/2))^2 ] or not ?](Q63213.png)
$$\mathrm{Sir},\:\mathrm{whether}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\left[\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}\right),\left(\frac{\mathrm{a}+\mathrm{b}}{\mathrm{2}}\right)^{\mathrm{2}} \right]\:\mathrm{or}\:\mathrm{not}\:? \\ $$
Answered by mr W last updated on 01/Jul/19
![tangent at P: m_T =2x_P normal at P: m_(NP) =−(1/m_T )=−(1/(2x_P )) m_(AP) =(x_P ^2 /(x_P −a)) m_(BP) =(x_P ^2 /(x_P −b)) 2θ_(NP) =(θ_(AP) +θ_(BP) ) ((2m_(NP) )/(1−m_(NP) ^2 ))=((m_(AP) +m_(BP) )/(1−m_(AP) m_(BP) )) ⇒((−(2/(2x_P )))/(1−(−(1/(2x_P )))^2 ))=(((x_P ^2 /(x_P −a))+(x_P ^2 /(x_P −b)))/(1−(x_P ^2 /(x_P −a))×(x_P ^2 /(x_P −b)))) ⇒−((4x_P )/(4x_P ^2 −1))=(((2x_P −a−b)x_P ^2 )/((x_P −a)(x_P −b)−x_P ^4 )) ⇒−(4/(4x_P ^2 −1))=(([2x_P −(a+b)]x_P )/(x_P ^2 +ab−(a+b)x_P −x_P ^4 )) ⇒−4ab+4(a+b)x_P −4x_P ^2 +4x_P ^4 =8x_P ^4 −2x_P ^2 −4(a+b)x_P ^3 +(a+b)x_P ⇒4x_P ^4 −4(a+b)x_P ^3 +2x_P ^2 −3(a+b)x_P +4ab=0 ⇒x_P ^4 −(a+b)x_P ^3 +(1/2)x_P ^2 −(3/4)(a+b)x_P +ab=0 x_P =....](Q63216.png)
$${tangent}\:{at}\:{P}: \\ $$$${m}_{{T}} =\mathrm{2}{x}_{{P}} \\ $$$${normal}\:{at}\:{P}: \\ $$$${m}_{{NP}} =−\frac{\mathrm{1}}{{m}_{{T}} }=−\frac{\mathrm{1}}{\mathrm{2}{x}_{{P}} } \\ $$$${m}_{{AP}} =\frac{{x}_{{P}} ^{\mathrm{2}} }{{x}_{{P}} −{a}} \\ $$$${m}_{{BP}} =\frac{{x}_{{P}} ^{\mathrm{2}} }{{x}_{{P}} −{b}} \\ $$$$\mathrm{2}\theta_{{NP}} =\left(\theta_{{AP}} +\theta_{{BP}} \right) \\ $$$$\frac{\mathrm{2}{m}_{{NP}} }{\mathrm{1}−{m}_{{NP}} ^{\mathrm{2}} }=\frac{{m}_{{AP}} +{m}_{{BP}} }{\mathrm{1}−{m}_{{AP}} {m}_{{BP}} } \\ $$$$\Rightarrow\frac{−\frac{\mathrm{2}}{\mathrm{2}{x}_{{P}} }}{\mathrm{1}−\left(−\frac{\mathrm{1}}{\mathrm{2}{x}_{{P}} }\right)^{\mathrm{2}} }=\frac{\frac{{x}_{{P}} ^{\mathrm{2}} }{{x}_{{P}} −{a}}+\frac{{x}_{{P}} ^{\mathrm{2}} }{{x}_{{P}} −{b}}}{\mathrm{1}−\frac{{x}_{{P}} ^{\mathrm{2}} }{{x}_{{P}} −{a}}×\frac{{x}_{{P}} ^{\mathrm{2}} }{{x}_{{P}} −{b}}} \\ $$$$\Rightarrow−\frac{\mathrm{4}{x}_{{P}} }{\mathrm{4}{x}_{{P}} ^{\mathrm{2}} −\mathrm{1}}=\frac{\left(\mathrm{2}{x}_{{P}} −{a}−{b}\right){x}_{{P}} ^{\mathrm{2}} }{\left({x}_{{P}} −{a}\right)\left({x}_{{P}} −{b}\right)−{x}_{{P}} ^{\mathrm{4}} } \\ $$$$\Rightarrow−\frac{\mathrm{4}}{\mathrm{4}{x}_{{P}} ^{\mathrm{2}} −\mathrm{1}}=\frac{\left[\mathrm{2}{x}_{{P}} −\left({a}+{b}\right)\right]{x}_{{P}} }{{x}_{{P}} ^{\mathrm{2}} +{ab}−\left({a}+{b}\right){x}_{{P}} −{x}_{{P}} ^{\mathrm{4}} } \\ $$$$\Rightarrow−\mathrm{4}{ab}+\mathrm{4}\left({a}+{b}\right){x}_{{P}} −\mathrm{4}{x}_{{P}} ^{\mathrm{2}} +\mathrm{4}{x}_{{P}} ^{\mathrm{4}} =\mathrm{8}{x}_{{P}} ^{\mathrm{4}} −\mathrm{2}{x}_{{P}} ^{\mathrm{2}} −\mathrm{4}\left({a}+{b}\right){x}_{{P}} ^{\mathrm{3}} +\left({a}+{b}\right){x}_{{P}} \\ $$$$\Rightarrow\mathrm{4}{x}_{{P}} ^{\mathrm{4}} −\mathrm{4}\left({a}+{b}\right){x}_{{P}} ^{\mathrm{3}} +\mathrm{2}{x}_{{P}} ^{\mathrm{2}} −\mathrm{3}\left({a}+{b}\right){x}_{{P}} +\mathrm{4}{ab}=\mathrm{0} \\ $$$$\Rightarrow{x}_{{P}} ^{\mathrm{4}} −\left({a}+{b}\right){x}_{{P}} ^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{2}}{x}_{{P}} ^{\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{4}}\left({a}+{b}\right){x}_{{P}} +{ab}=\mathrm{0} \\ $$$${x}_{{P}} =.... \\ $$
Commented by ajfour last updated on 01/Jul/19
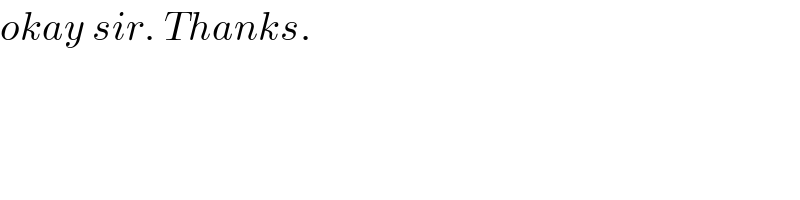
$${okay}\:{sir}.\:{Thanks}. \\ $$
Commented by MJS last updated on 01/Jul/19
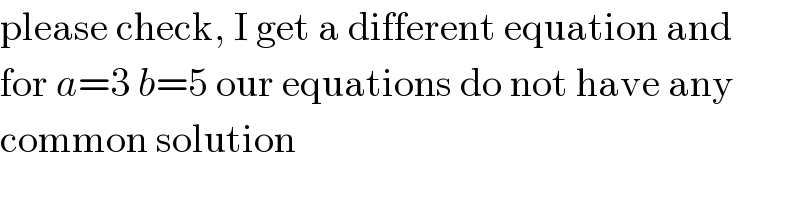
$$\mathrm{please}\:\mathrm{check},\:\mathrm{I}\:\mathrm{get}\:\mathrm{a}\:\mathrm{different}\:\mathrm{equation}\:\mathrm{and} \\ $$$$\mathrm{for}\:{a}=\mathrm{3}\:{b}=\mathrm{5}\:\mathrm{our}\:\mathrm{equations}\:\mathrm{do}\:\mathrm{not}\:\mathrm{have}\:\mathrm{any} \\ $$$$\mathrm{common}\:\mathrm{solution} \\ $$
Commented by mr W last updated on 01/Jul/19

$${thank}\:{you}\:{sir}!\:{a}\:{typo}\:{led}\:{to}\:{wrong} \\ $$$${equation}\:{in}\:{my}\:{working}.\:{now}\:{it}'{s}\:{fixed}. \\ $$
Commented by MJS last updated on 01/Jul/19

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$$$\mathrm{I}\:\mathrm{thought}\:\mathrm{there}\:\mathrm{must}\:\mathrm{be}\:\mathrm{a}\:\mathrm{typo}\:\mathrm{because}\:\mathrm{your} \\ $$$$\mathrm{path}\:\mathrm{seemed}\:\mathrm{right} \\ $$
Answered by MJS last updated on 01/Jul/19
![P= ((x),(x^2 ) ) ∣AP∣+∣BP∣=(√(x^4 +x^2 −2ax+a^2 ))+(√(x^4 +x^2 −2bx+b^2 )) (d/dx)[(√(x^4 +x^2 −2ax+a^2 ))+(√(x^4 +x^2 −2bx+b^2 ))]=0 ((2x^3 +x−a)/(√(x^4 +x^2 −2ax+a^2 )))+((2x^3 +x−b)/(√(x^4 +x^2 −2bx+b^2 )))=0 after squaring and transforming we get x^4 −(a+b)x^3 +(1/2)x^2 −((3(a+b))/4)x+ab=0](Q63252.png)
$${P}=\begin{pmatrix}{{x}}\\{{x}^{\mathrm{2}} }\end{pmatrix} \\ $$$$\mid{AP}\mid+\mid{BP}\mid=\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} −\mathrm{2}{ax}+{a}^{\mathrm{2}} }+\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} −\mathrm{2}{bx}+{b}^{\mathrm{2}} } \\ $$$$\frac{{d}}{{dx}}\left[\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} −\mathrm{2}{ax}+{a}^{\mathrm{2}} }+\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} −\mathrm{2}{bx}+{b}^{\mathrm{2}} }\right]=\mathrm{0} \\ $$$$\frac{\mathrm{2}{x}^{\mathrm{3}} +{x}−{a}}{\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} −\mathrm{2}{ax}+{a}^{\mathrm{2}} }}+\frac{\mathrm{2}{x}^{\mathrm{3}} +{x}−{b}}{\sqrt{{x}^{\mathrm{4}} +{x}^{\mathrm{2}} −\mathrm{2}{bx}+{b}^{\mathrm{2}} }}=\mathrm{0} \\ $$$$\mathrm{after}\:\mathrm{squaring}\:\mathrm{and}\:\mathrm{transforming}\:\mathrm{we}\:\mathrm{get} \\ $$$${x}^{\mathrm{4}} −\left({a}+{b}\right){x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} −\frac{\mathrm{3}\left({a}+{b}\right)}{\mathrm{4}}{x}+{ab}=\mathrm{0} \\ $$
