
Question Number 63162 by Rio Michael last updated on 29/Jun/19
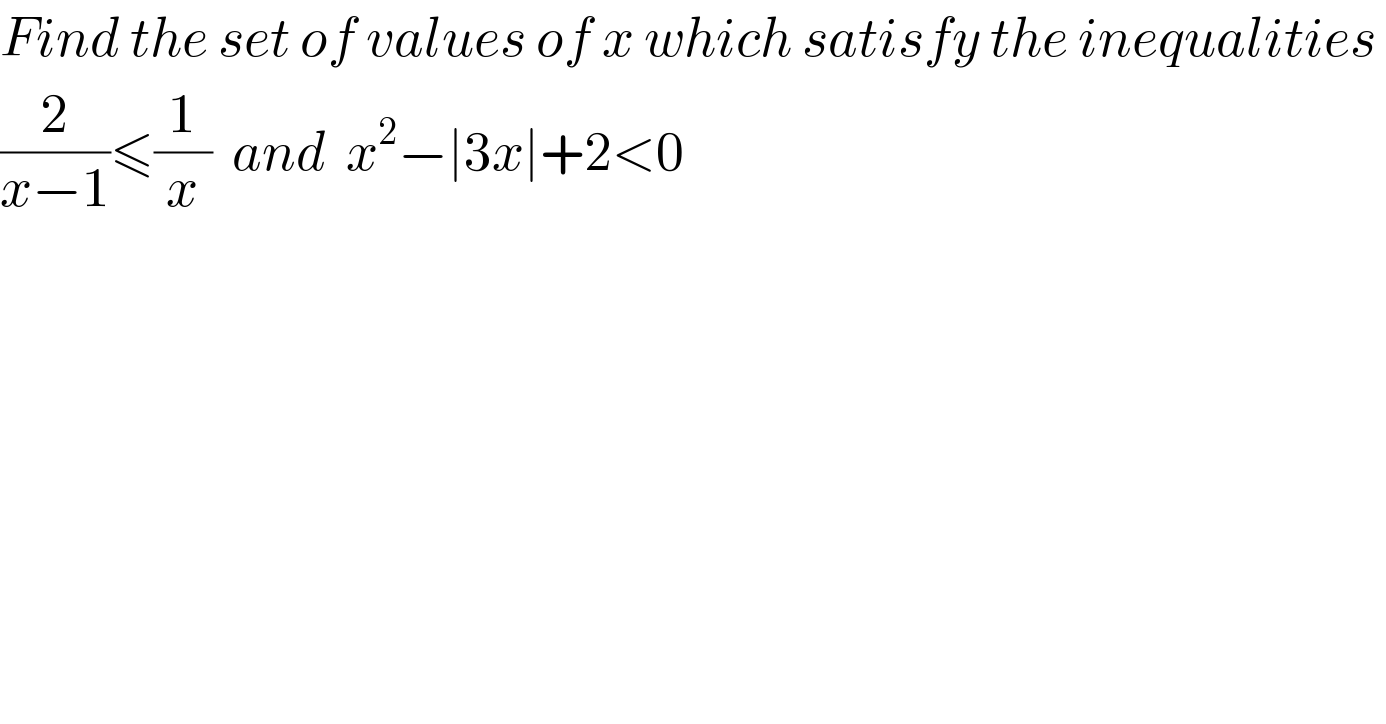
$${Find}\:{the}\:{set}\:{of}\:{values}\:{of}\:{x}\:{which}\:{satisfy}\:{the}\:{inequalities}\: \\ $$ $$\frac{\mathrm{2}}{{x}−\mathrm{1}}\leqslant\frac{\mathrm{1}}{{x}}\:\:{and}\:\:{x}^{\mathrm{2}} −\mid\mathrm{3}{x}\mid+\mathrm{2}<\mathrm{0} \\ $$
Commented byPrithwish sen last updated on 30/Jun/19

$$\frac{\mathrm{2}}{\mathrm{x}−\mathrm{1}}\leqslant\frac{\mathrm{1}}{\mathrm{x}}\:\Rightarrow\mathrm{x}\leqslant−\mathrm{1} \\ $$ $$\mathrm{x}^{\mathrm{2}} −\mid\mathrm{3x}\mid\:+\mathrm{2}\:<\mathrm{0}\:\:\Rightarrow\:\mathrm{x}^{\mathrm{2}} +\mathrm{3x}+\mathrm{2}<\:\mathrm{0}\:\left(\:\because\:\mathrm{x}\leqslant−\mathrm{1}\right) \\ $$ $$\mathrm{i}.\mathrm{e}\:\left(\mathrm{x}+\mathrm{1}\right)\left(\mathrm{x}+\mathrm{2}\right)<\:\mathrm{0} \\ $$ $$\mathrm{either}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{or} \\ $$ $$\:\:\left(\mathrm{x}+\mathrm{1}\right)<\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{x}+\mathrm{1}\right)>\mathrm{0} \\ $$ $$\mathrm{and}\left(\mathrm{x}+\mathrm{2}\right)>\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{and}\:\left(\mathrm{x}+\mathrm{2}\right)<\:\mathrm{0} \\ $$ $$\Rightarrow\:−\mathrm{2}<\mathrm{x}<−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:−\mathrm{1}<\mathrm{x}<−\mathrm{2}\: \\ $$ $$\because\:\mathrm{x}\leqslant\:−\mathrm{1}\:\:\therefore\:\:\mathrm{the}\:\mathrm{only}\:\mathrm{possible}\:\mathrm{solution}\:\mathrm{is} \\ $$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}<\mathrm{x}<−\mathrm{1} \\ $$ $$\mathrm{please}\:\mathrm{check}\:\mathrm{the}\:\mathrm{answer}. \\ $$
Commented byRio Michael last updated on 02/Jul/19
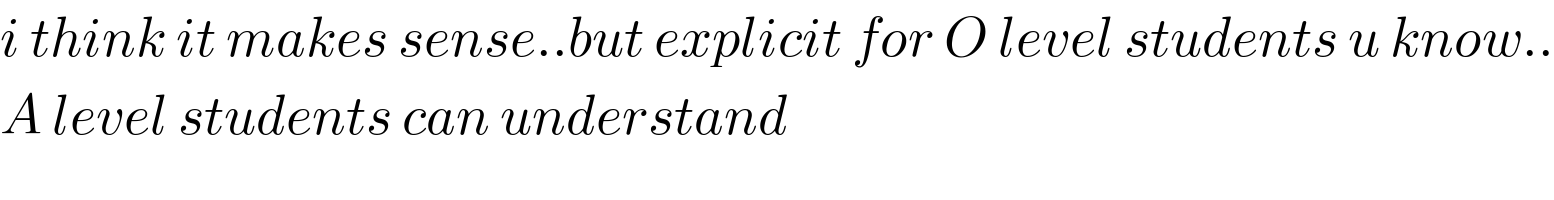
$${i}\:{think}\:{it}\:{makes}\:{sense}..{but}\:{explicit}\:{for}\:{O}\:{level}\:{students}\:{u}\:{know}.. \\ $$ $${A}\:{level}\:{students}\:{can}\:{understand} \\ $$
Commented bymathmax by abdo last updated on 30/Jun/19
![(e_1 ) for x≠0 and x≠1 (2/(x−1)) ≤(1/x) ⇔(2/(x−1)) −(1/x) ≤0 ⇒((2x−x+1)/(x(x−1))) ≤0 ⇒ ((x+1)/(x(x−1))) ≤0 x −∞ −1 0 1 +∞ x+1 − 0 + + + x(x−1) + + 0 − 0 + ((x+1)/(x(x−1) )) − + − + ⇒ D_1 = ]−∞ ,−1] ∪ ]0,1[ (e_2 ) x^2 −3∣x∣ +2 <0 ⇒∣x∣−3∣x∣ +2 <0 Δ =9−8 =1 ⇒ ∣x∣_1 =((3+1)/2) =2 ⇒x =+^− 2 ∣x∣_2 =((3−1)/2) =1 ⇒x =+^− 1 ⇒x^2 −3∣x∣+2 =(∣x∣−1)(∣x∣−2) (e_2 ) ⇒ (∣x∣−1)(∣x∣−2) <0 ⇒∣x∣ ∈]1,2[ ⇒ 1<∣x∣<2 1<∣x∣ ⇒x>1 or x<−1 ⇒x ∈]−∞,−1[∪]1,+∞[ ∣x∣<2 ⇒−2<x<2 ⇒ ∩ =]−2,−1[∪]1,2[ =D_2 ⇒ D =D_1 ∩D_2 =....](Q63212.png)
$$\left({e}_{\mathrm{1}} \right)\:{for}\:{x}\neq\mathrm{0}\:{and}\:{x}\neq\mathrm{1}\:\:\:\:\frac{\mathrm{2}}{{x}−\mathrm{1}}\:\leqslant\frac{\mathrm{1}}{{x}}\:\Leftrightarrow\frac{\mathrm{2}}{{x}−\mathrm{1}}\:−\frac{\mathrm{1}}{{x}}\:\leqslant\mathrm{0}\:\Rightarrow\frac{\mathrm{2}{x}−{x}+\mathrm{1}}{{x}\left({x}−\mathrm{1}\right)}\:\leqslant\mathrm{0}\:\Rightarrow \\ $$ $$\frac{{x}+\mathrm{1}}{{x}\left({x}−\mathrm{1}\right)}\:\leqslant\mathrm{0} \\ $$ $${x}\:\:\:\:\:\:\:\:\:\:−\infty\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\infty \\ $$ $${x}+\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\:\:\:\:+ \\ $$ $${x}\left({x}−\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\:−\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:+ \\ $$ $$\frac{{x}+\mathrm{1}}{{x}\left({x}−\mathrm{1}\right)\:\:\:\:}\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:−\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+ \\ $$ $$\left.\Rightarrow\left.\:\left.{D}_{\mathrm{1}} =\:\right]−\infty\:,−\mathrm{1}\right]\:\cup\:\:\right]\mathrm{0},\mathrm{1}\left[\right. \\ $$ $$\left({e}_{\mathrm{2}} \right)\:\:\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} −\mathrm{3}\mid{x}\mid\:+\mathrm{2}\:<\mathrm{0}\:\Rightarrow\mid{x}\mid−\mathrm{3}\mid{x}\mid\:+\mathrm{2}\:<\mathrm{0} \\ $$ $$\Delta\:=\mathrm{9}−\mathrm{8}\:=\mathrm{1}\:\:\Rightarrow\:\mid{x}\mid_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{1}}{\mathrm{2}}\:=\mathrm{2}\:\Rightarrow{x}\:=\overset{−} {+}\mathrm{2} \\ $$ $$\mid{x}\mid_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{1}}{\mathrm{2}}\:=\mathrm{1}\:\Rightarrow{x}\:=\overset{−} {+}\mathrm{1}\:\Rightarrow{x}^{\mathrm{2}} −\mathrm{3}\mid{x}\mid+\mathrm{2}\:=\left(\mid{x}\mid−\mathrm{1}\right)\left(\mid{x}\mid−\mathrm{2}\right) \\ $$ $$\left.\left({e}_{\mathrm{2}} \right)\:\Rightarrow\:\left(\mid{x}\mid−\mathrm{1}\right)\left(\mid{x}\mid−\mathrm{2}\right)\:<\mathrm{0}\:\:\Rightarrow\mid{x}\mid\:\in\right]\mathrm{1},\mathrm{2}\left[\:\Rightarrow\:\mathrm{1}<\mid{x}\mid<\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\right. \\ $$ $$\left.\mathrm{1}<\mid{x}\mid\:\Rightarrow{x}>\mathrm{1}\:{or}\:{x}<−\mathrm{1}\:\Rightarrow{x}\:\in\right]−\infty,−\mathrm{1}\left[\cup\right]\mathrm{1},+\infty\left[\right. \\ $$ $$\left.\mid{x}\mid<\mathrm{2}\:\Rightarrow−\mathrm{2}<{x}<\mathrm{2}\:\Rightarrow\:\cap\:=\right]−\mathrm{2},−\mathrm{1}\left[\cup\right]\mathrm{1},\mathrm{2}\left[\:={D}_{\mathrm{2}} \:\Rightarrow\right. \\ $$ $${D}\:={D}_{\mathrm{1}} \cap{D}_{\mathrm{2}} =.... \\ $$
Answered by ajfour last updated on 30/Jun/19
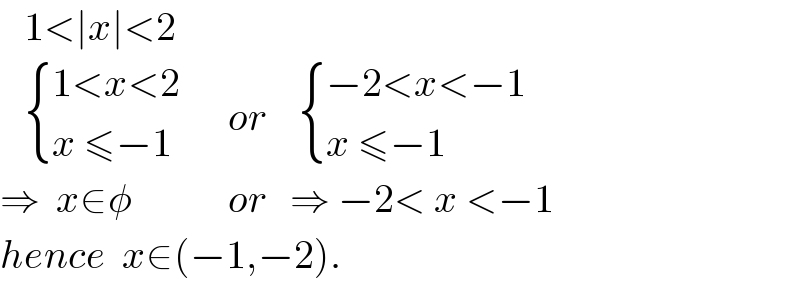
$$\:\:\:\mathrm{1}<\mid{x}\mid<\mathrm{2} \\ $$ $$\:\:\:\begin{cases}{\mathrm{1}<{x}<\mathrm{2}}\\{{x}\:\leqslant−\mathrm{1}}\end{cases}\:\:\:\:\:\:{or}\:\:\:\:\begin{cases}{−\mathrm{2}<{x}<−\mathrm{1}}\\{{x}\:\leqslant−\mathrm{1}}\end{cases} \\ $$ $$\Rightarrow\:\:{x}\in\phi\:\:\:\:\:\:\:\:\:\:\:\:{or}\:\:\:\Rightarrow\:−\mathrm{2}<\:{x}\:<−\mathrm{1} \\ $$ $${hence}\:\:{x}\in\left(−\mathrm{1},−\mathrm{2}\right). \\ $$
