
Question Number 63116 by mugan deni last updated on 29/Jun/19
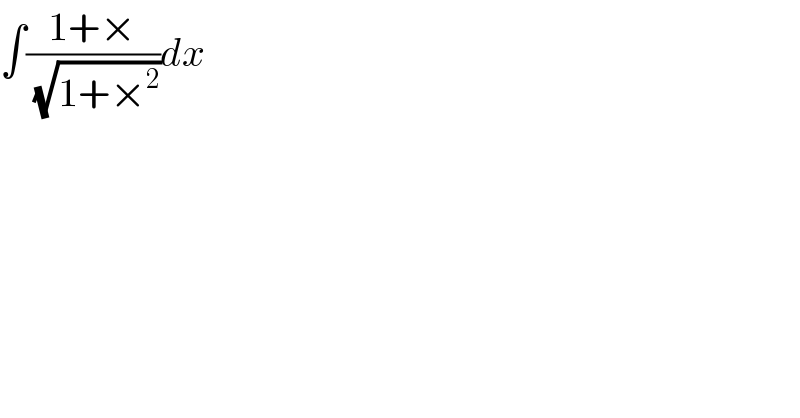
$$\int\frac{\mathrm{1}+×}{\sqrt{\mathrm{1}+×^{\mathrm{2}} }}{dx} \\ $$
Commented by mathmax by abdo last updated on 30/Jun/19

$${let}\:{use}\:{the}\:{changement}\:{x}={tan}\theta\:\Rightarrow \\ $$$$\int\:\frac{\mathrm{1}+{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{dx}\:=\int\:\:\frac{\mathrm{1}+{tan}\theta}{\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta\:=\:\int\:\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\left(\mathrm{1}+{tan}\theta\right){d}\theta \\ $$$$=\int\:\:\frac{\mathrm{1}+{tan}\theta}{{cos}\theta}\:{d}\theta=\int\:\:\frac{{d}\theta}{{cos}\theta}\:+\:\int\:\:\:\frac{{sin}\theta}{{cos}^{\mathrm{2}} \theta}\:{d}\theta \\ $$$$\int\:\:\:\frac{{sin}\theta}{{cos}^{\mathrm{2}} \theta}\:=\frac{\mathrm{1}}{{cos}\theta}\:+{c}_{\mathrm{1}} \\ $$$$\int\:\:\frac{{d}\theta}{{cos}\theta}\:=_{{tan}\left(\frac{\theta}{\mathrm{2}}\right)={u}} \:\:\:\:\:\int\:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}\:=\int\:\:\:\frac{\mathrm{2}{du}}{\mathrm{1}−{u}^{\mathrm{2}} }\:=\int\:\left(\frac{\mathrm{1}}{\mathrm{1}−{u}}\:+\frac{\mathrm{1}}{\mathrm{1}+{u}}\right){du} \\ $$$$={ln}\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid\:+{c}_{\mathrm{2}} ={ln}\mid\frac{\mathrm{1}+{tan}\left(\frac{\theta}{\mathrm{2}}\right)}{\mathrm{1}−{tan}\left(\frac{\theta}{\mathrm{2}}\right)}\mid\:+{c}_{\mathrm{2}} ={ln}\mid{tan}\left(\frac{\pi}{\mathrm{4}}+\frac{\theta}{\mathrm{2}}\right)\mid\:\Rightarrow \\ $$$${we}\:{have}\:\:\mathrm{1}+{x}^{\mathrm{2}} \:=\frac{\mathrm{1}}{{cos}^{\mathrm{2}} \theta}\:\Rightarrow\:{cos}^{\mathrm{2}} \theta\:=\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\:\Rightarrow{cos}\theta\:=\frac{\mathrm{1}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:\Rightarrow \\ $$$$\int\:\:\frac{\mathrm{1}+{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx}\:=\sqrt{\mathrm{1}+{x}^{\mathrm{2}} \:}\:\:+{ln}\mid{tan}\left(\frac{\pi}{\mathrm{4}}+\frac{{arctanx}}{\mathrm{2}}\right)\mid\:+{C} \\ $$$${another}\:{way} \\ $$$$\int\:\:\frac{\mathrm{1}+{x}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{dx}\:=\int\:\:\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:+\int\:\:\:\:\frac{{xdx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}={ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+{C}\right. \\ $$$${and}\:{this}\:{way}\:\:{is}\:{eazy}... \\ $$
Answered by Hope last updated on 29/Jun/19
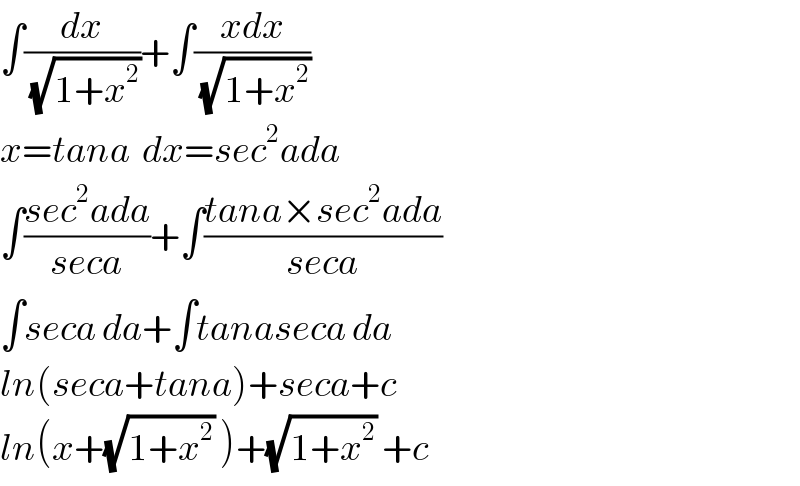
$$\int\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}+\int\frac{{xdx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }} \\ $$$${x}={tana}\:\:{dx}={sec}^{\mathrm{2}} {ada} \\ $$$$\int\frac{{sec}^{\mathrm{2}} {ada}}{{seca}}+\int\frac{{tana}×{sec}^{\mathrm{2}} {ada}}{{seca}} \\ $$$$\int{seca}\:{da}+\int{tanaseca}\:{da} \\ $$$${ln}\left({seca}+{tana}\right)+{seca}+{c} \\ $$$${ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:\right)+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+{c} \\ $$
