
Question Number 6311 by FilupSmith last updated on 23/Jun/16
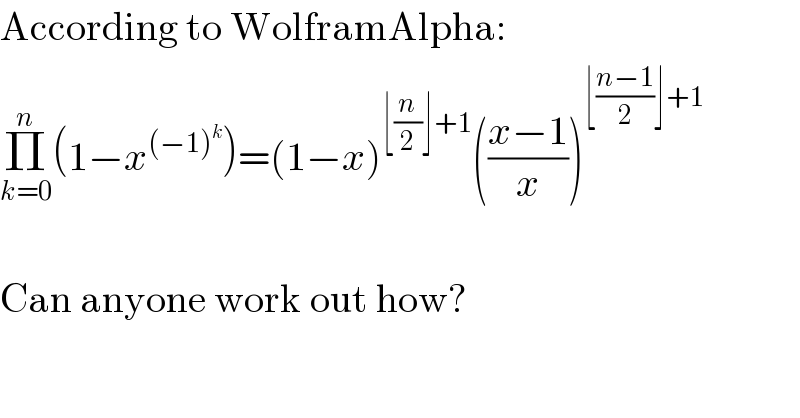
$$\mathrm{According}\:\mathrm{to}\:\mathrm{WolframAlpha}: \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\prod}}\left(\mathrm{1}−{x}^{\left(−\mathrm{1}\right)^{{k}} } \right)=\left(\mathrm{1}−{x}\right)^{\lfloor\frac{{n}}{\mathrm{2}}\rfloor+\mathrm{1}} \left(\frac{{x}−\mathrm{1}}{{x}}\right)^{\lfloor\frac{{n}−\mathrm{1}}{\mathrm{2}}\rfloor+\mathrm{1}} \\ $$$$ \\ $$$$\mathrm{Can}\:\mathrm{anyone}\:\mathrm{work}\:\mathrm{out}\:\mathrm{how}? \\ $$
Commented by FilupSmith last updated on 24/Jun/16

$$\mathrm{Amazing}! \\ $$
Commented by Yozzii last updated on 23/Jun/16

$${Let}\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\prod}}\left(\mathrm{1}−{x}^{\left(−\mathrm{1}\right)^{{k}} } \right)=\phi,\:{n}\in\mathbb{Z}^{\geqslant} \:\left({x}\neq\mathrm{0}\right) \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$$\left(\mathrm{I}\right)\:{For}\:{n}\:{being}\:{even},\:{let}\:{n}=\mathrm{2}{r},\:{r}\in\mathbb{Z}^{\geqslant} . \\ $$$${r}=\frac{{n}}{\mathrm{2}}.\:{As}\:{k}\:{varies}\:{from}\:{k}=\mathrm{0}\:{to}\:{k}=\mathrm{2}{r}, \\ $$$${r}\:{terms}\:{in}\:{the}\:{product}\:{will} \\ $$$${have}\:{k}=\mathrm{2}{t}−\mathrm{1}\left({t}\in\mathbb{N}\right)\Rightarrow\left(\mathrm{1}−{x}^{\left(−\mathrm{1}\right)^{{k}} } \right)=\mathrm{1}−\frac{\mathrm{1}}{{x}}=\frac{{x}−\mathrm{1}}{{x}}, \\ $$$${and}\:{the}\:{remaining}\:{r}+\mathrm{1}\:{terms}\:{will}\:{have} \\ $$$${k}=\mathrm{2}{t}\Rightarrow\:\left(\mathrm{1}−{x}^{\left(−\mathrm{1}\right)^{{k}} } \right)=\mathrm{1}−{x}. \\ $$$${So},\:{we}\:{may}\:{write}\: \\ $$$$\phi=\left\{\underset{{k}\in\mathbb{E},\mathrm{0}\leqslant{k}\leqslant{n}} {\prod}\left(\mathrm{1}−{x}^{\left(−\mathrm{1}\right)^{{k}} } \right)\right\}\left\{\underset{{k}\in\mathbb{O},\mathrm{0}\leqslant{k}\leqslant{n}} {\prod}\left(\mathrm{1}−{x}^{\left(−\mathrm{1}\right)^{{k}} } \right)\right\} \\ $$$$\phi=\left(\mathrm{1}−{x}\right)^{{r}+\mathrm{1}} ×\left(\frac{{x}−\mathrm{1}}{{x}}\right)^{{r}} \:{or} \\ $$$$\phi=\left(\mathrm{1}−{x}\right)^{\frac{{n}}{\mathrm{2}}+\mathrm{1}} \left(\frac{{x}−\mathrm{1}}{{x}}\right)^{\frac{{n}}{\mathrm{2}}} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$$\left(\mathrm{II}\right)\:{If}\:{n}\:{is}\:{odd}\:{then}\:{let}\:{n}=\mathrm{2}{r}+\mathrm{1},\:{r}\in\mathbb{Z}^{\geqslant} . \\ $$$${There}\:{will}\:{be}\:{r}+\mathrm{1}\:{terms}\:{with}\:{odd}\:{k} \\ $$$${and}\:{r}+\mathrm{1}\:{terms}\:{with}\:{even}\:{k}. \\ $$$${So}\:{we}\:{can}\:{write},\:{similarly}\:{to}\:{above}, \\ $$$$\phi=\left(\mathrm{1}−{x}\right)^{{r}+\mathrm{1}} \left(\frac{{x}−\mathrm{1}}{{x}}\right)^{{r}+\mathrm{1}} \\ $$$${or}\:\phi=\left(\mathrm{1}−{x}\right)^{\frac{{n}−\mathrm{1}}{\mathrm{2}}+\mathrm{1}} \left(\frac{{x}−\mathrm{1}}{{x}}\right)^{\frac{{n}−\mathrm{1}}{\mathrm{2}}+\mathrm{1}} \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Now},\:{if}\:{n}\:{is}\:{even}\:{then}\:{truly}\:\lfloor\frac{{n}}{\mathrm{2}}\rfloor=\frac{{n}}{\mathrm{2}} \\ $$$$\Rightarrow\lfloor\frac{{n}}{\mathrm{2}}\rfloor+\mathrm{1}=\frac{{n}}{\mathrm{2}}+\mathrm{1}.\:{So},\:{this}\:{is}\:{an}\:{identity}\:{for}\:{part}\:\left(\mathrm{I}\right)\: \\ $$$${for}\:{the}\:{term}\:\left(\mathrm{1}−{x}\right)^{\frac{{n}}{\mathrm{2}}+\mathrm{1}} .\: \\ $$$${Also},\:{n}−\mathrm{1}=\mathrm{2}{r}+\mathrm{1}\:{for}\:{some}\:{r}\in\mathbb{Z}^{\geqslant} . \\ $$$$\Rightarrow\frac{{n}−\mathrm{1}}{\mathrm{2}}={r}+\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\lfloor\frac{{n}−\mathrm{1}}{\mathrm{2}}\rfloor={r}\Rightarrow\lfloor\frac{{n}−\mathrm{1}}{\mathrm{2}}\rfloor+\mathrm{1}={r}+\mathrm{1}=\frac{{n}−\mathrm{2}}{\mathrm{2}}+\mathrm{1}=\frac{{n}}{\mathrm{2}}. \\ $$$${Hence},\:{we}\:{can}\:{use}\:\lfloor\frac{{n}−\mathrm{1}}{\mathrm{2}}\rfloor+\mathrm{1}\:{instead}\:{of}\:\frac{{n}}{\mathrm{2}} \\ $$$${for}\:{the}\:{term}\:\left(\frac{{x}−\mathrm{1}}{{x}}\right)^{{n}/\mathrm{2}} . \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${If}\:{n}\:{is}\:{odd}\:{then}\:{for}\:{n}=\mathrm{2}{r}+\mathrm{1}\: \\ $$$$\Rightarrow\frac{{n}}{\mathrm{2}}={r}+\frac{\mathrm{1}}{\mathrm{2}}\Rightarrow\lfloor\frac{{n}}{\mathrm{2}}\rfloor={r}\Rightarrow\lfloor\frac{{n}}{\mathrm{2}}\rfloor+\mathrm{1}={r}+\mathrm{1}=\frac{{n}−\mathrm{1}}{\mathrm{2}}+\mathrm{1}. \\ $$$${Therefore},\:{this}\:{is}\:{an}\:{identity}\:{for} \\ $$$${the}\:{term}\:\left(\mathrm{1}−{x}\right)^{\frac{{n}−\mathrm{1}}{\mathrm{2}}+\mathrm{1}} \:{in}\:{part}\:\left(\mathrm{II}\right). \\ $$$${For}\:{n}=\mathrm{2}{r}+\mathrm{1}\Rightarrow{n}−\mathrm{1}=\mathrm{2}{r}\Rightarrow\frac{{n}−\mathrm{1}}{\mathrm{2}}={r} \\ $$$$\Rightarrow\lfloor\frac{{n}−\mathrm{1}}{\mathrm{2}}\rfloor={r}\Rightarrow\lfloor\frac{{n}−\mathrm{1}}{\mathrm{2}}\rfloor+\mathrm{1}={r}+\mathrm{1}=\frac{{n}−\mathrm{1}}{\mathrm{2}}+\mathrm{1}. \\ $$$${Thus},\:{for}\:{the}\:{term}\:{in}\:\left(\frac{{x}−\mathrm{1}}{{x}}\right)^{\frac{{n}−\mathrm{1}}{\mathrm{2}}+\mathrm{1}} \\ $$$${we}\:{can}\:{write}\:\left(\frac{{x}−\mathrm{1}}{{x}}\right)^{\lfloor\frac{{n}−\mathrm{1}}{\mathrm{2}}\rfloor+\mathrm{1}} \:{instead}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Notice}\:{in}\:{the}\:{both}\:{cases},\:\left(\mathrm{I}\right)\:{and}\:\left(\mathrm{II}\right),\: \\ $$$${we}\:{can}\:{write}\:\left(\mathrm{1}−{x}\right)^{\lfloor\frac{{n}}{\mathrm{2}}\rfloor+\mathrm{1}} \:{and}\:\left(\frac{{x}−\mathrm{1}}{{x}}\right)^{\lfloor\frac{{n}−\mathrm{1}}{\mathrm{2}}\rfloor+\mathrm{1}} \\ $$$${in}\:{the}\:{result}\:{of}\:\phi\:{for}\:{any}\:{n}\in\mathbb{Z}^{\geqslant} . \\ $$$$\therefore\:{Generally},\:{for}\:{x}\neq\mathrm{0}\:{and}\:{n}\in\mathbb{Z}^{\geqslant} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\prod}}\left(\mathrm{1}−{x}^{\left(−\mathrm{1}\right)^{{k}} } \right)=\left(\mathrm{1}−{x}\right)^{\lfloor\frac{{n}}{\mathrm{2}}\rfloor+\mathrm{1}} \left(\frac{{x}−\mathrm{1}}{{x}}\right)^{\lfloor\frac{{n}−\mathrm{1}}{\mathrm{2}}\rfloor+\mathrm{1}} .\:\left({Shown}\right) \\ $$
Commented by FilupSmith last updated on 23/Jun/16
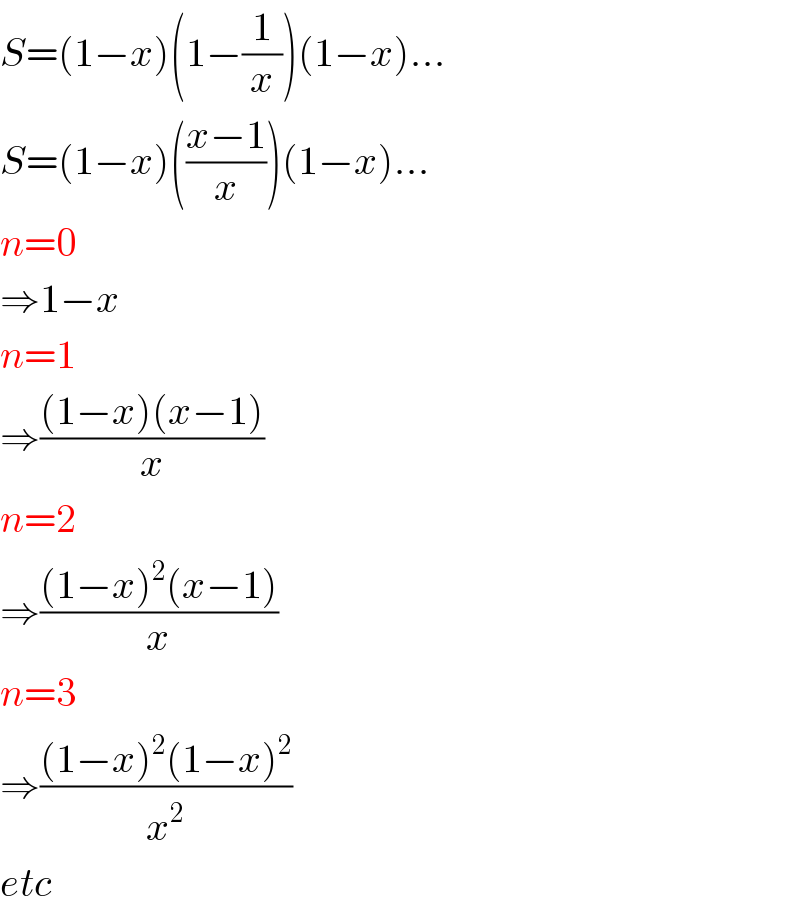
$${S}=\left(\mathrm{1}−{x}\right)\left(\mathrm{1}−\frac{\mathrm{1}}{{x}}\right)\left(\mathrm{1}−{x}\right)... \\ $$$${S}=\left(\mathrm{1}−{x}\right)\left(\frac{{x}−\mathrm{1}}{{x}}\right)\left(\mathrm{1}−{x}\right)... \\ $$$${n}=\mathrm{0} \\ $$$$\Rightarrow\mathrm{1}−{x} \\ $$$${n}=\mathrm{1} \\ $$$$\Rightarrow\frac{\left(\mathrm{1}−{x}\right)\left({x}−\mathrm{1}\right)}{{x}} \\ $$$${n}=\mathrm{2} \\ $$$$\Rightarrow\frac{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} \left({x}−\mathrm{1}\right)}{{x}} \\ $$$${n}=\mathrm{3} \\ $$$$\Rightarrow\frac{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} \left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{{x}^{\mathrm{2}} } \\ $$$${etc} \\ $$
