
Previous in Relation and Functions Next in Relation and Functions
Question Number 63101 by mathmax by abdo last updated on 29/Jun/19
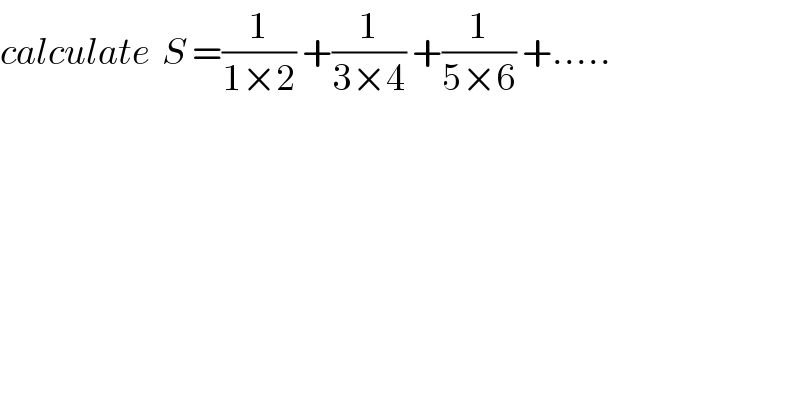
$${calculate}\:\:{S}\:=\frac{\mathrm{1}}{\mathrm{1}×\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}×\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{5}×\mathrm{6}}\:+..... \\ $$
Commented by mathmax by abdo last updated on 29/Jun/19
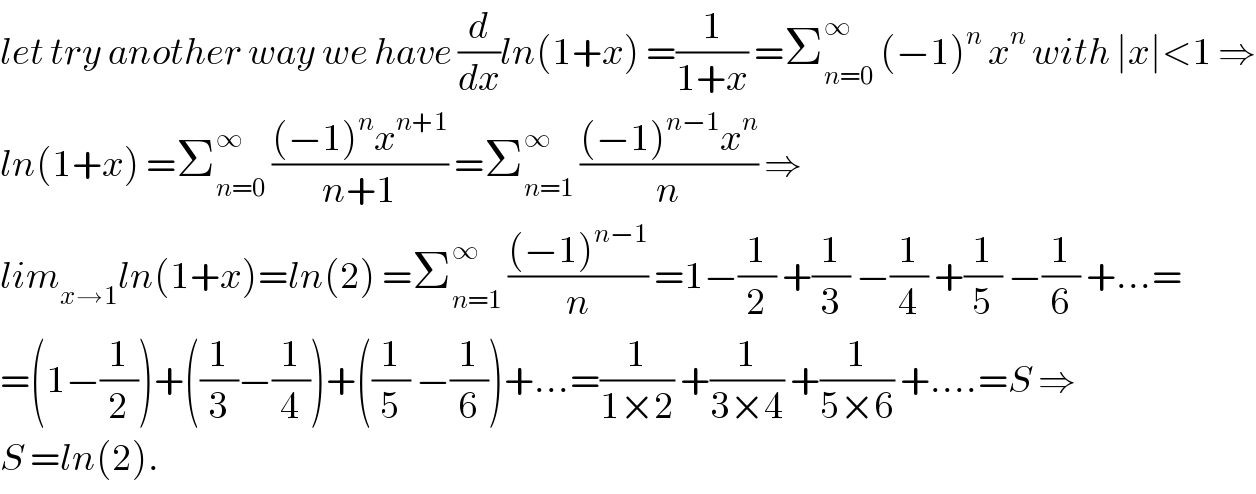
$${let}\:{try}\:{another}\:{way}\:{we}\:{have}\:\frac{{d}}{{dx}}{ln}\left(\mathrm{1}+{x}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{{n}} \:{x}^{{n}} \:{with}\:\mid{x}\mid<\mathrm{1}\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+{x}\right)\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {x}^{{n}} }{{n}}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{1}} {ln}\left(\mathrm{1}+{x}\right)={ln}\left(\mathrm{2}\right)\:=\sum_{{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{5}}\:−\frac{\mathrm{1}}{\mathrm{6}}\:+...= \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}\right)+\left(\frac{\mathrm{1}}{\mathrm{5}}\:−\frac{\mathrm{1}}{\mathrm{6}}\right)+...=\frac{\mathrm{1}}{\mathrm{1}×\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}×\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{5}×\mathrm{6}}\:+....={S}\:\Rightarrow \\ $$$${S}\:={ln}\left(\mathrm{2}\right). \\ $$
Answered by mr W last updated on 29/Jun/19
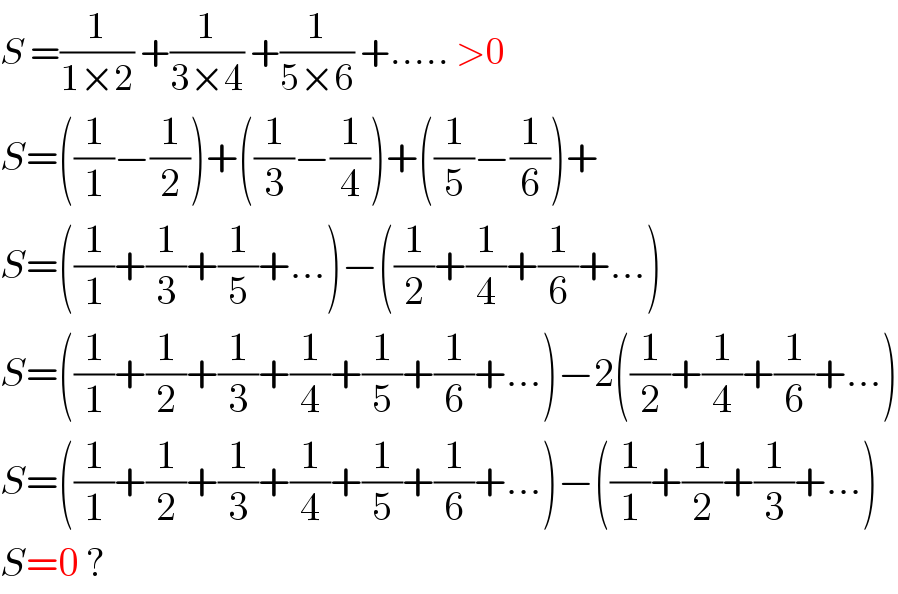
$${S}\:=\frac{\mathrm{1}}{\mathrm{1}×\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}×\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{5}×\mathrm{6}}\:+.....\:>\mathrm{0} \\ $$$${S}=\left(\frac{\mathrm{1}}{\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\right)+\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{4}}\right)+\left(\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{6}}\right)+ \\ $$$${S}=\left(\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{5}}+...\right)−\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{6}}+...\right) \\ $$$${S}=\left(\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{6}}+...\right)−\mathrm{2}\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{6}}+...\right) \\ $$$${S}=\left(\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{6}}+...\right)−\left(\frac{\mathrm{1}}{\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}+...\right) \\ $$$${S}=\mathrm{0}\:? \\ $$
Commented by MJS last updated on 29/Jun/19
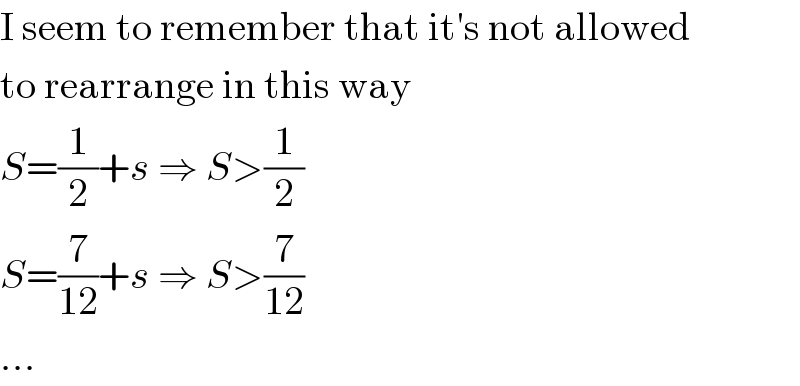
$$\mathrm{I}\:\mathrm{seem}\:\mathrm{to}\:\mathrm{remember}\:\mathrm{that}\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{allowed} \\ $$$$\mathrm{to}\:\mathrm{rearrange}\:\mathrm{in}\:\mathrm{this}\:\mathrm{way} \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{2}}+{s}\:\Rightarrow\:{S}>\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${S}=\frac{\mathrm{7}}{\mathrm{12}}+{s}\:\Rightarrow\:{S}>\frac{\mathrm{7}}{\mathrm{12}} \\ $$$$... \\ $$
Commented by turbo msup by abdo last updated on 29/Jun/19
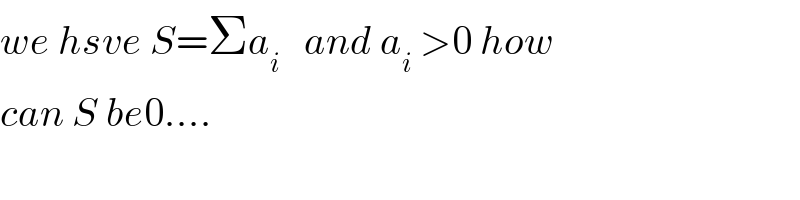
$${we}\:{hsve}\:{S}=\Sigma{a}_{{i}} \:\:\:{and}\:{a}_{{i}} \:>\mathrm{0}\:{how} \\ $$$${can}\:{S}\:{be}\mathrm{0}.... \\ $$
Commented by turbo msup by abdo last updated on 29/Jun/19
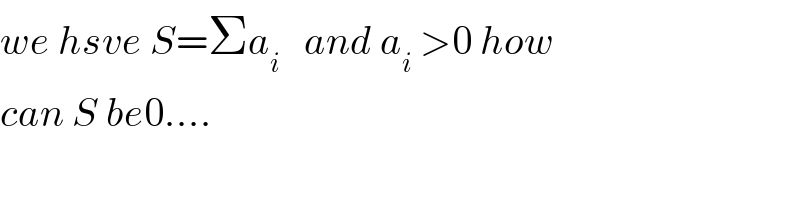
$${we}\:{hsve}\:{S}=\Sigma{a}_{{i}} \:\:\:{and}\:{a}_{{i}} \:>\mathrm{0}\:{how} \\ $$$${can}\:{S}\:{be}\mathrm{0}.... \\ $$
Commented by mathmax by abdo last updated on 29/Jun/19

$${sir}\:{mrw}\:{your}\:{begining}\:{is}\:{correct}\:\:{but}\:{the}\:{answer}\:{is}\:{not}\:\mathrm{0}\:{let}\:{complete}\:{the} \\ $$$${work}\:{we}\:{have}\:{S}\:={lim}_{{n}\rightarrow+\infty} \left(\:\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\right) \\ $$$${we}\:{have}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:={H}_{{n}} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{5}}\:+....+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{5}}\:+....+\frac{\mathrm{1}}{\mathrm{2}{n}}\:+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}} \\ $$$$−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{4}}\:−....−\frac{\mathrm{1}}{\mathrm{2}{n}}\:={H}_{\mathrm{2}{n}+\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} \:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{\mathrm{2}{k}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:={H}_{\mathrm{2}{n}+\mathrm{1}} −{H}_{{n}} ={ln}\left(\mathrm{2}{n}+\mathrm{1}\right)+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)−{ln}\left({n}\right)−\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$$={ln}\left(\frac{\mathrm{2}{n}+\mathrm{1}}{{n}}\right)+{o}\left(\frac{\mathrm{1}}{{n}}\right)\rightarrow{ln}\left(\mathrm{2}\right)\:\left({n}\rightarrow+\infty\right)\:{so} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}×\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}×\mathrm{4}}\:+\frac{\mathrm{1}}{\mathrm{5}×\mathrm{6}}\:+.....={ln}\left(\mathrm{2}\right).\left(\gamma\:{is}\:{the}\:{constant}\:{of}\:{euler}\right) \\ $$
Commented by mr W last updated on 29/Jun/19
$${thanks}\:{sir}!\:{i}\:{learnt}\:{something}\:{new}. \\ $$
Commented by mathmax by abdo last updated on 29/Jun/19
$${you}\:{are}\:{always}\:{welcome}. \\ $$
Answered by MJS last updated on 29/Jun/19
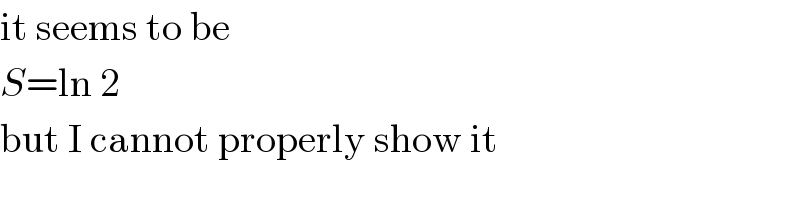
$$\mathrm{it}\:\mathrm{seems}\:\mathrm{to}\:\mathrm{be} \\ $$$${S}=\mathrm{ln}\:\mathrm{2} \\ $$$$\mathrm{but}\:\mathrm{I}\:\mathrm{cannot}\:\mathrm{properly}\:\mathrm{show}\:\mathrm{it} \\ $$
Answered by naka3546 last updated on 29/Jun/19

