
Question Number 63090 by ajfour last updated on 28/Jun/19
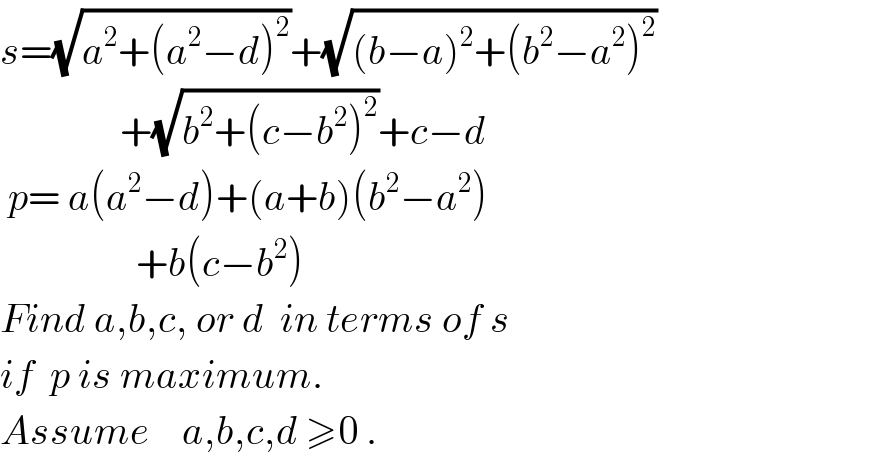
$${s}=\sqrt{{a}^{\mathrm{2}} +\left({a}^{\mathrm{2}} −{d}\right)^{\mathrm{2}} }+\sqrt{\left({b}−{a}\right)^{\mathrm{2}} +\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\sqrt{{b}^{\mathrm{2}} +\left({c}−{b}^{\mathrm{2}} \right)^{\mathrm{2}} }+{c}−{d} \\ $$$$\:{p}=\:{a}\left({a}^{\mathrm{2}} −{d}\right)+\left({a}+{b}\right)\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{b}\left({c}−{b}^{\mathrm{2}} \right) \\ $$$${Find}\:{a},{b},{c},\:{or}\:{d}\:\:{in}\:{terms}\:{of}\:{s} \\ $$$${if}\:\:{p}\:{is}\:{maximum}.\: \\ $$$${Assume}\:\:\:\:{a},{b},{c},{d}\:\geqslant\mathrm{0}\:. \\ $$
