
Question Number 63065 by Enebeli Chinedu Vitalis last updated on 28/Jun/19
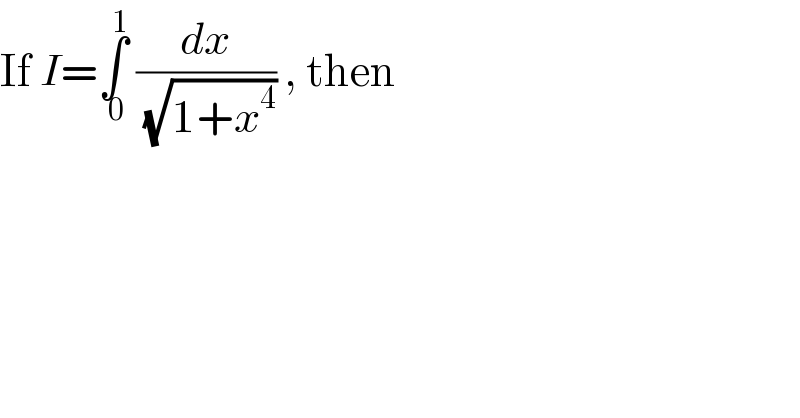
$$\mathrm{If}\:{I}=\underset{\:\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }}\:,\:\mathrm{then} \\ $$
Commented by Enebeli Chinedu Vitalis last updated on 28/Jun/19

$${thanks}\:{boss}\bigstar\bigstar \\ $$
Commented by mathmax by abdo last updated on 28/Jun/19

$${changement}\:{x}^{\mathrm{2}} ={tan}\theta\:{give}\:{x}\:=\left({tan}\theta\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right)\left({tan}\theta\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} {d}\theta \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\:\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\left({tan}\theta\right)^{−\frac{\mathrm{1}}{\mathrm{2}}} \:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{\mathrm{1}}{{cos}\theta\:\sqrt{\frac{{sin}\theta}{{cos}\theta}}}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{d}\theta}{\sqrt{{cos}\theta{sin}\theta}} \\ $$$$=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:\frac{{d}\theta}{\sqrt{{sin}\left(\mathrm{2}\theta\right)}}\:=\frac{\mathrm{1}}{\sqrt{\mathrm{2}}}\int_{\mathrm{0}} ^{\pi} \:\:\:\frac{{dt}}{\mathrm{2}\sqrt{{sint}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{2}\theta={t}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\pi} \:\:\:\:\:\frac{{dt}}{\sqrt{{sint}}}\:\:{changement}\:\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)\:={u}\:{give} \\ $$$$\int_{\mathrm{0}} ^{\pi} \:\:\frac{{dt}}{\sqrt{{sint}}}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\:\:\frac{\mathrm{2}{du}}{\left(\mathrm{1}+{u}^{\mathrm{2}} \right)\sqrt{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}}\:=\sqrt{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \:\:\:\:\:\:\frac{{du}}{\sqrt{{u}}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }} \\ $$$$=_{\sqrt{{u}}=\alpha} \:\:\:\:\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\mathrm{2}\alpha{d}\alpha}{\alpha\sqrt{\mathrm{1}+\alpha^{\mathrm{4}} }}\:\:=\mathrm{2}\sqrt{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{d}\alpha}{\sqrt{\mathrm{1}+\alpha^{\mathrm{4}} }}\:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }} \\ $$$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }}\:+\:\int_{\mathrm{1}} ^{+\infty} \:\:\:\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }}\:\Rightarrow\:\int_{\mathrm{1}} ^{+\infty} \:\:\frac{{dx}}{\sqrt{\mathrm{1}+{x}^{\mathrm{4}} }}\:=\mathrm{0}....{be}\:{contnued}.... \\ $$
Commented by mathmax by abdo last updated on 28/Jun/19

$${you}\:{are}\:{welcome}. \\ $$
