
Question Number 63032 by mathmax by abdo last updated on 28/Jun/19
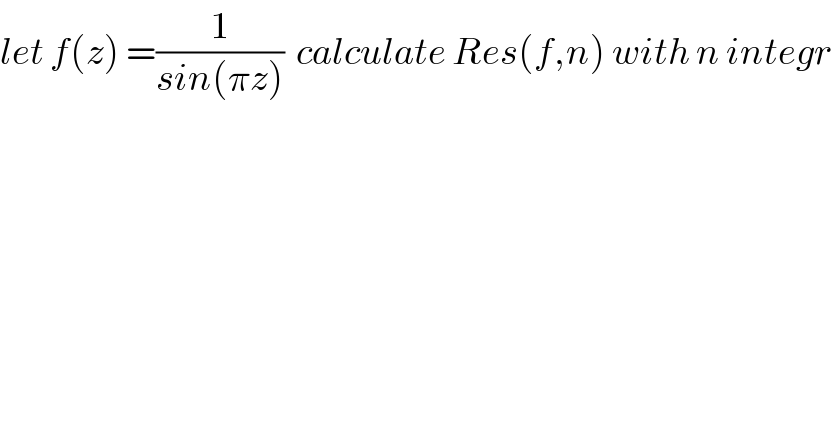
$${let}\:{f}\left({z}\right)\:=\frac{\mathrm{1}}{{sin}\left(\pi{z}\right)}\:\:{calculate}\:{Res}\left({f},{n}\right)\:{with}\:{n}\:{integr} \\ $$
Commented by mathmax by abdo last updated on 28/Jun/19
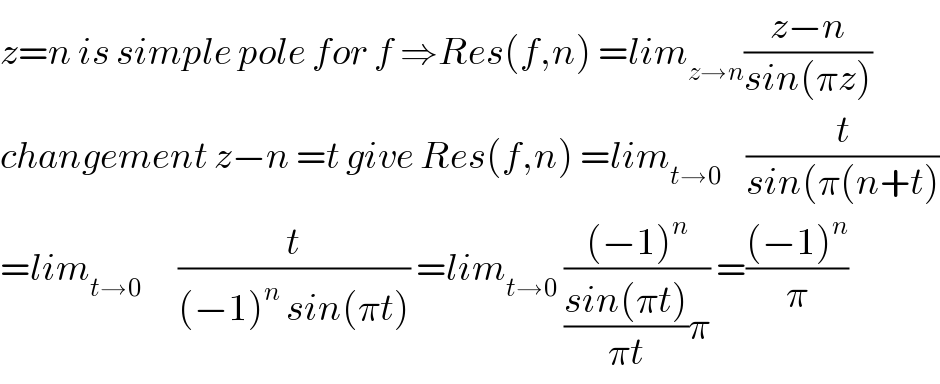
$${z}={n}\:{is}\:{simple}\:{pole}\:{for}\:{f}\:\Rightarrow{Res}\left({f},{n}\right)\:={lim}_{{z}\rightarrow{n}} \frac{{z}−{n}}{{sin}\left(\pi{z}\right)} \\ $$$${changement}\:{z}−{n}\:={t}\:{give}\:{Res}\left({f},{n}\right)\:={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\:\frac{{t}}{{sin}\left(\pi\left({n}+{t}\right)\right.} \\ $$$$={lim}_{{t}\rightarrow\mathrm{0}} \:\:\:\:\:\:\frac{{t}}{\left(−\mathrm{1}\right)^{{n}} \:{sin}\left(\pi{t}\right)}\:={lim}_{{t}\rightarrow\mathrm{0}} \:\frac{\left(−\mathrm{1}\right)^{{n}} }{\frac{{sin}\left(\pi{t}\right)}{\pi{t}}\pi}\:=\frac{\left(−\mathrm{1}\right)^{{n}} }{\pi} \\ $$
