
Question Number 62938 by ajfour last updated on 27/Jun/19
Commented by ajfour last updated on 27/Jun/19
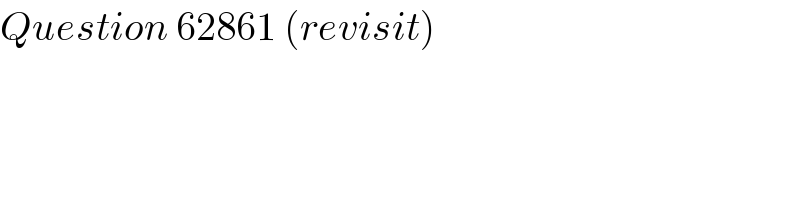
$${Question}\:\mathrm{62861}\:\left({revisit}\right) \\ $$
Answered by ajfour last updated on 27/Jun/19
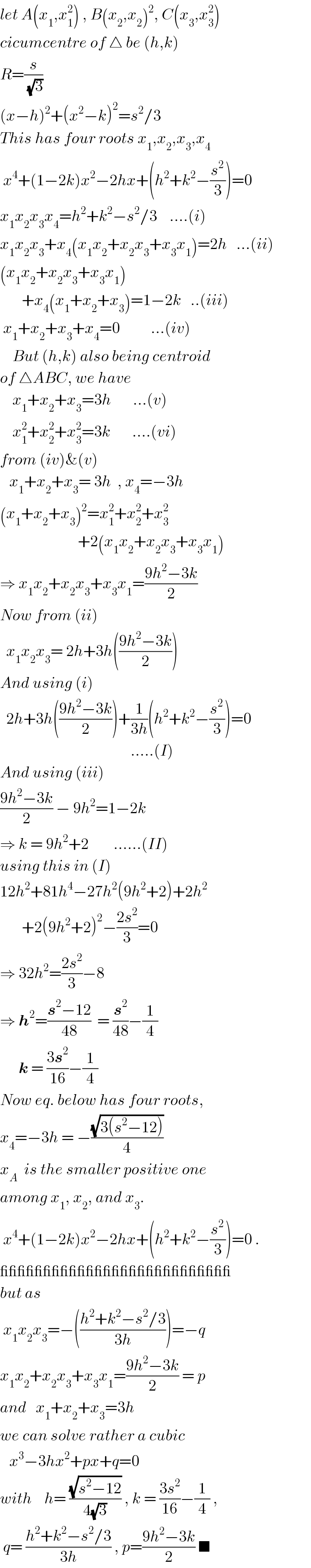
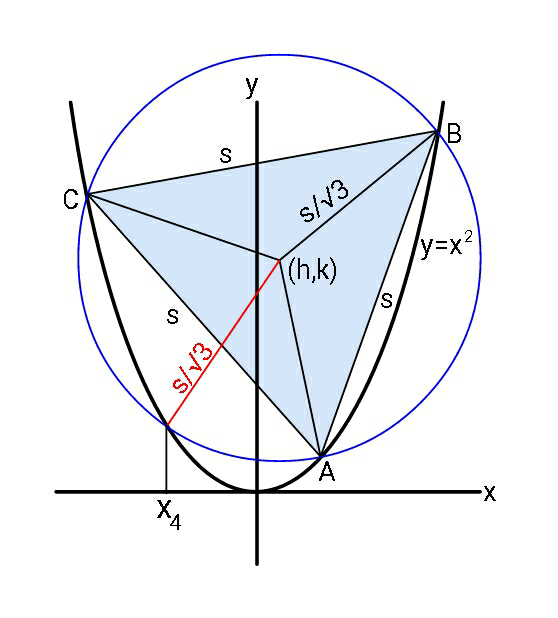
$${let}\:{A}\left({x}_{\mathrm{1}} ,{x}_{\mathrm{1}} ^{\mathrm{2}} \right)\:,\:{B}\left({x}_{\mathrm{2}} ,{x}_{\mathrm{2}} \right)^{\mathrm{2}} ,\:{C}\left({x}_{\mathrm{3}} ,{x}_{\mathrm{3}} ^{\mathrm{2}} \right) \\ $$$${cicumcentre}\:{of}\:\bigtriangleup\:{be}\:\left({h},{k}\right) \\ $$$${R}=\frac{{s}}{\sqrt{\mathrm{3}}} \\ $$$$\left({x}−{h}\right)^{\mathrm{2}} +\left({x}^{\mathrm{2}} −{k}\right)^{\mathrm{2}} ={s}^{\mathrm{2}} /\mathrm{3} \\ $$$${This}\:{has}\:{four}\:{roots}\:{x}_{\mathrm{1}} ,{x}_{\mathrm{2}} ,{x}_{\mathrm{3}} ,{x}_{\mathrm{4}} \\ $$$$\:{x}^{\mathrm{4}} +\left(\mathrm{1}−\mathrm{2}{k}\right){x}^{\mathrm{2}} −\mathrm{2}{hx}+\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} −\frac{{s}^{\mathrm{2}} }{\mathrm{3}}\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} {x}_{\mathrm{4}} ={h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{s}^{\mathrm{2}} /\mathrm{3}\:\:\:\:....\left({i}\right) \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} +{x}_{\mathrm{4}} \left({x}_{\mathrm{1}} {x}_{\mathrm{2}} +{x}_{\mathrm{2}} {x}_{\mathrm{3}} +{x}_{\mathrm{3}} {x}_{\mathrm{1}} \right)=\mathrm{2}{h}\:\:\:...\left({ii}\right) \\ $$$$\left({x}_{\mathrm{1}} {x}_{\mathrm{2}} +{x}_{\mathrm{2}} {x}_{\mathrm{3}} +{x}_{\mathrm{3}} {x}_{\mathrm{1}} \right)\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:+{x}_{\mathrm{4}} \left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} \right)=\mathrm{1}−\mathrm{2}{k}\:\:\:..\left({iii}\right) \\ $$$$\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} +{x}_{\mathrm{4}} =\mathrm{0}\:\:\:\:\:\:\:\:\:\:...\left({iv}\right) \\ $$$$\:\:\:\:{But}\:\left({h},{k}\right)\:{also}\:{being}\:{centroid} \\ $$$${of}\:\bigtriangleup{ABC},\:{we}\:{have} \\ $$$$\:\:\:\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} =\mathrm{3}{h}\:\:\:\:\:\:\:...\left({v}\right) \\ $$$$\:\:\:\:{x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} =\mathrm{3}{k}\:\:\:\:\:\:\:....\left({vi}\right) \\ $$$${from}\:\left({iv}\right)\&\left({v}\right) \\ $$$$\:\:\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} =\:\mathrm{3}{h}\:\:,\:{x}_{\mathrm{4}} =−\mathrm{3}{h} \\ $$$$\left({x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} \right)^{\mathrm{2}} ={x}_{\mathrm{1}} ^{\mathrm{2}} +{x}_{\mathrm{2}} ^{\mathrm{2}} +{x}_{\mathrm{3}} ^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mathrm{2}\left({x}_{\mathrm{1}} {x}_{\mathrm{2}} +{x}_{\mathrm{2}} {x}_{\mathrm{3}} +{x}_{\mathrm{3}} {x}_{\mathrm{1}} \right) \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} {x}_{\mathrm{2}} +{x}_{\mathrm{2}} {x}_{\mathrm{3}} +{x}_{\mathrm{3}} {x}_{\mathrm{1}} =\frac{\mathrm{9}{h}^{\mathrm{2}} −\mathrm{3}{k}}{\mathrm{2}} \\ $$$${Now}\:{from}\:\left({ii}\right) \\ $$$$\:\:{x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} =\:\mathrm{2}{h}+\mathrm{3}{h}\left(\frac{\mathrm{9}{h}^{\mathrm{2}} −\mathrm{3}{k}}{\mathrm{2}}\right) \\ $$$${And}\:{using}\:\left({i}\right) \\ $$$$\:\:\mathrm{2}{h}+\mathrm{3}{h}\left(\frac{\mathrm{9}{h}^{\mathrm{2}} −\mathrm{3}{k}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{3}{h}}\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} −\frac{{s}^{\mathrm{2}} }{\mathrm{3}}\right)=\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:.....\left({I}\right) \\ $$$${And}\:{using}\:\left({iii}\right) \\ $$$$\frac{\mathrm{9}{h}^{\mathrm{2}} −\mathrm{3}{k}}{\mathrm{2}}\:−\:\mathrm{9}{h}^{\mathrm{2}} =\mathrm{1}−\mathrm{2}{k} \\ $$$$\Rightarrow\:{k}\:=\:\mathrm{9}{h}^{\mathrm{2}} +\mathrm{2}\:\:\:\:\:\:\:\:......\left({II}\right) \\ $$$${using}\:{this}\:{in}\:\left({I}\right) \\ $$$$\mathrm{12}{h}^{\mathrm{2}} +\mathrm{81}{h}^{\mathrm{4}} −\mathrm{27}{h}^{\mathrm{2}} \left(\mathrm{9}{h}^{\mathrm{2}} +\mathrm{2}\right)+\mathrm{2}{h}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:+\mathrm{2}\left(\mathrm{9}{h}^{\mathrm{2}} +\mathrm{2}\right)^{\mathrm{2}} −\frac{\mathrm{2}{s}^{\mathrm{2}} }{\mathrm{3}}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{32}{h}^{\mathrm{2}} =\frac{\mathrm{2}{s}^{\mathrm{2}} }{\mathrm{3}}−\mathrm{8} \\ $$$$\Rightarrow\:\boldsymbol{{h}}^{\mathrm{2}} =\frac{\boldsymbol{{s}}^{\mathrm{2}} −\mathrm{12}}{\mathrm{48}}\:\:=\:\frac{\boldsymbol{{s}}^{\mathrm{2}} }{\mathrm{48}}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\boldsymbol{{k}}\:=\:\frac{\mathrm{3}\boldsymbol{{s}}^{\mathrm{2}} }{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${Now}\:{eq}.\:{below}\:{has}\:{four}\:{roots}, \\ $$$${x}_{\mathrm{4}} =−\mathrm{3}{h}\:=\:−\frac{\sqrt{\mathrm{3}\left({s}^{\mathrm{2}} −\mathrm{12}\right)}}{\mathrm{4}} \\ $$$${x}_{{A}} \:\:{is}\:{the}\:{smaller}\:{positive}\:{one} \\ $$$${among}\:{x}_{\mathrm{1}} ,\:{x}_{\mathrm{2}} ,\:{and}\:{x}_{\mathrm{3}} . \\ $$$$\:{x}^{\mathrm{4}} +\left(\mathrm{1}−\mathrm{2}{k}\right){x}^{\mathrm{2}} −\mathrm{2}{hx}+\left({h}^{\mathrm{2}} +{k}^{\mathrm{2}} −\frac{{s}^{\mathrm{2}} }{\mathrm{3}}\right)=\mathrm{0}\:. \\ $$$$\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_ \\ $$$${but}\:{as} \\ $$$$\:{x}_{\mathrm{1}} {x}_{\mathrm{2}} {x}_{\mathrm{3}} =−\left(\frac{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{s}^{\mathrm{2}} /\mathrm{3}}{\mathrm{3}{h}}\right)=−{q} \\ $$$${x}_{\mathrm{1}} {x}_{\mathrm{2}} +{x}_{\mathrm{2}} {x}_{\mathrm{3}} +{x}_{\mathrm{3}} {x}_{\mathrm{1}} =\frac{\mathrm{9}{h}^{\mathrm{2}} −\mathrm{3}{k}}{\mathrm{2}}\:=\:{p} \\ $$$${and}\:\:\:{x}_{\mathrm{1}} +{x}_{\mathrm{2}} +{x}_{\mathrm{3}} =\mathrm{3}{h} \\ $$$${we}\:{can}\:{solve}\:{rather}\:{a}\:{cubic} \\ $$$$\:\:\:{x}^{\mathrm{3}} −\mathrm{3}{hx}^{\mathrm{2}} +{px}+{q}=\mathrm{0}\: \\ $$$${with}\:\:\:\:{h}=\:\frac{\sqrt{{s}^{\mathrm{2}} −\mathrm{12}}}{\mathrm{4}\sqrt{\mathrm{3}}}\:,\:{k}\:=\:\frac{\mathrm{3}{s}^{\mathrm{2}} }{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{4}}\:, \\ $$$$\:{q}=\:\frac{{h}^{\mathrm{2}} +{k}^{\mathrm{2}} −{s}^{\mathrm{2}} /\mathrm{3}}{\mathrm{3}{h}}\:,\:{p}=\frac{\mathrm{9}{h}^{\mathrm{2}} −\mathrm{3}{k}}{\mathrm{2}}\:\blacksquare \\ $$
Commented by mr W last updated on 27/Jun/19
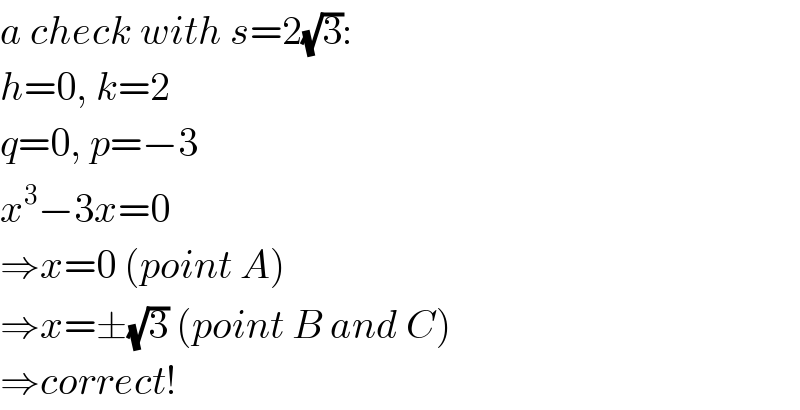
$${a}\:{check}\:{with}\:{s}=\mathrm{2}\sqrt{\mathrm{3}}: \\ $$$${h}=\mathrm{0},\:{k}=\mathrm{2} \\ $$$${q}=\mathrm{0},\:{p}=−\mathrm{3} \\ $$$${x}^{\mathrm{3}} −\mathrm{3}{x}=\mathrm{0}\: \\ $$$$\Rightarrow{x}=\mathrm{0}\:\left({point}\:{A}\right) \\ $$$$\Rightarrow{x}=\pm\sqrt{\mathrm{3}}\:\left({point}\:{B}\:{and}\:{C}\right) \\ $$$$\Rightarrow{correct}! \\ $$
Commented by mr W last updated on 27/Jun/19
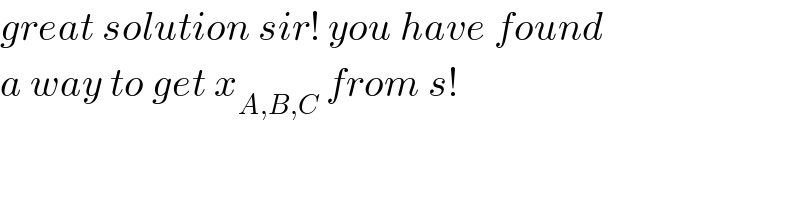
$${great}\:{solution}\:{sir}!\:{you}\:{have}\:{found} \\ $$$${a}\:{way}\:{to}\:{get}\:{x}_{{A},{B},{C}} \:{from}\:{s}! \\ $$
Commented by ajfour last updated on 27/Jun/19
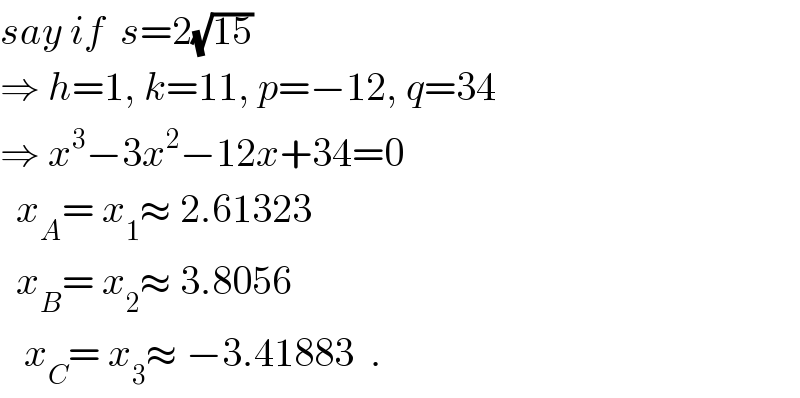
$${say}\:{if}\:\:{s}=\mathrm{2}\sqrt{\mathrm{15}} \\ $$$$\Rightarrow\:{h}=\mathrm{1},\:{k}=\mathrm{11},\:{p}=−\mathrm{12},\:{q}=\mathrm{34} \\ $$$$\Rightarrow\:{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} −\mathrm{12}{x}+\mathrm{34}=\mathrm{0} \\ $$$$\:\:{x}_{{A}} =\:{x}_{\mathrm{1}} \approx\:\mathrm{2}.\mathrm{61323} \\ $$$$\:\:{x}_{{B}} =\:{x}_{\mathrm{2}} \approx\:\mathrm{3}.\mathrm{8056} \\ $$$$\:\:\:{x}_{{C}} =\:{x}_{\mathrm{3}} \approx\:−\mathrm{3}.\mathrm{41883}\:\:. \\ $$
Commented by ajfour last updated on 27/Jun/19
Thank you sir, it only needed our focus on center of triangle which is centroid as well as circumcenter.
Commented by mr W last updated on 28/Jun/19
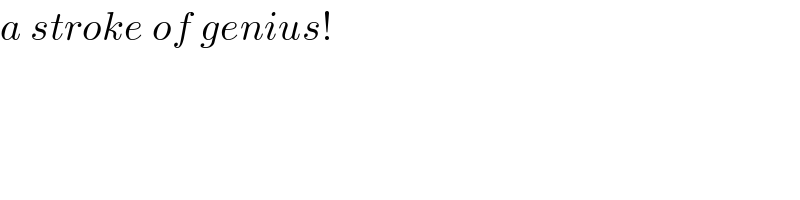
$${a}\:{stroke}\:{of}\:{genius}! \\ $$
