
Question Number 62761 by lalitchand last updated on 25/Jun/19
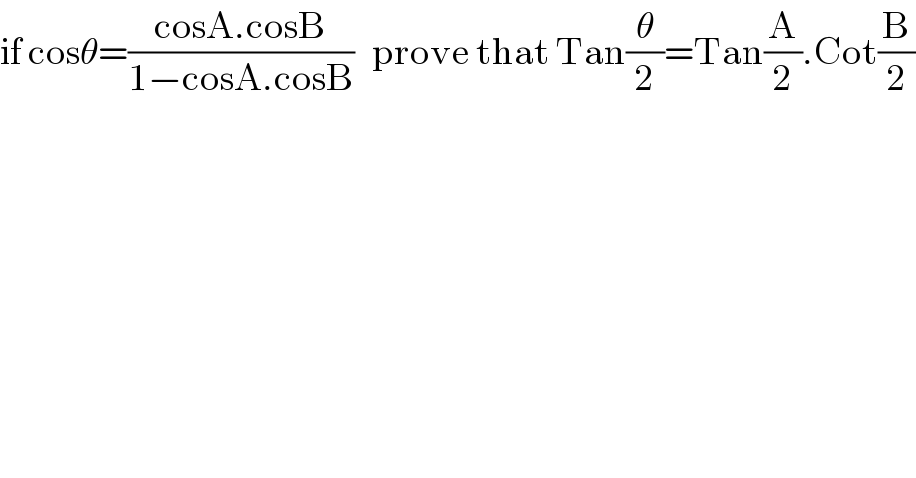
$$\mathrm{if}\:\mathrm{cos}\theta=\frac{\mathrm{cosA}.\mathrm{cosB}}{\mathrm{1}−\mathrm{cosA}.\mathrm{cosB}}\:\:\:\mathrm{prove}\:\mathrm{that}\:\mathrm{Tan}\frac{\theta}{\mathrm{2}}=\mathrm{Tan}\frac{\mathrm{A}}{\mathrm{2}}.\mathrm{Cot}\frac{\mathrm{B}}{\mathrm{2}} \\ $$
Commented by Prithwish sen last updated on 25/Jun/19

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{is} \\ $$$$\mathrm{cos}\theta\:=\:\frac{\mathrm{cosA}−\mathrm{cosB}}{\mathrm{1}−\mathrm{cosAcosB}} \\ $$$$\frac{\mathrm{1}−\mathrm{cos}\theta}{\mathrm{1}+\mathrm{cos}\theta}\:=\:\frac{\mathrm{1}−\mathrm{cosA}+\mathrm{cosB}−\mathrm{cosAcosB}}{\mathrm{1}+\mathrm{cosA}−\mathrm{cosB}−\mathrm{cosAcosB}} \\ $$$$\mathrm{tan}\frac{\theta}{\mathrm{2}\:}\:\:=\:\frac{\left(\mathrm{1}−\mathrm{cosA}\right)\left(\mathrm{1}+\mathrm{cosB}\right)}{\left(\mathrm{1}+\mathrm{cosA}\right)\left(\mathrm{1}−\mathrm{cosB}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{tan}\frac{\mathrm{A}}{\mathrm{2}}.\mathrm{cot}\frac{\mathrm{B}}{\mathrm{2}} \\ $$$$\mathrm{waiting}\:\mathrm{for}\:\mathrm{your}\:\mathrm{comment}. \\ $$
Commented by lalitchand last updated on 25/Jun/19

$$\mathrm{is}\:\mathrm{that}\:\mathrm{question}\:\mathrm{is}\:\mathrm{wrong}??\:\mathrm{and}\:\mathrm{u}\:\mathrm{have}\:\mathrm{applied} \\ $$$$\mathrm{componendo}\:\mathrm{and}\:\mathrm{dividedendo}\:\mathrm{after}\:\mathrm{reciporcal} \\ $$
Commented by Prithwish sen last updated on 25/Jun/19

$$\mathrm{I}\:\mathrm{think}\:\mathrm{so}. \\ $$
