
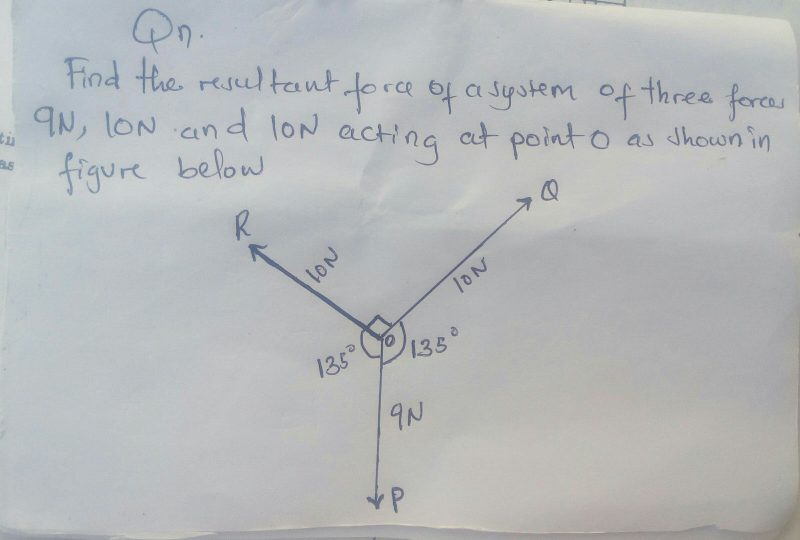
Question Number 62624 by Jmasanja last updated on 23/Jun/19
Answered by MJS last updated on 23/Jun/19
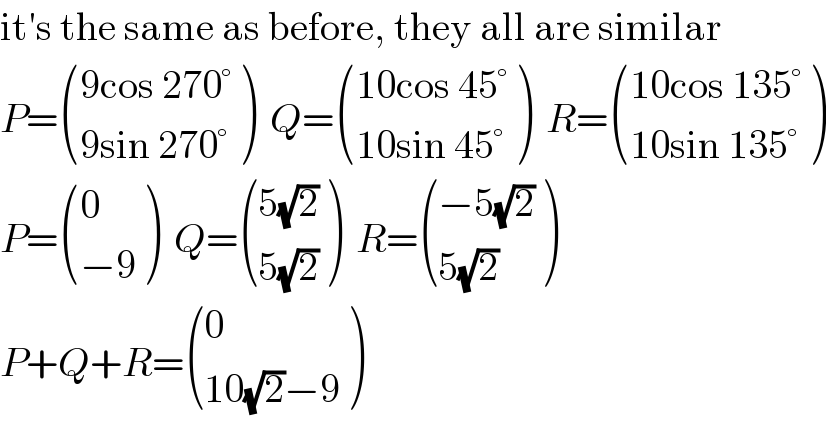
$$\mathrm{it}'\mathrm{s}\:\mathrm{the}\:\mathrm{same}\:\mathrm{as}\:\mathrm{before},\:\mathrm{they}\:\mathrm{all}\:\mathrm{are}\:\mathrm{similar} \\ $$$${P}=\begin{pmatrix}{\mathrm{9cos}\:\mathrm{270}°}\\{\mathrm{9sin}\:\mathrm{270}°}\end{pmatrix}\:\:{Q}=\begin{pmatrix}{\mathrm{10cos}\:\mathrm{45}°}\\{\mathrm{10sin}\:\mathrm{45}°}\end{pmatrix}\:\:{R}=\begin{pmatrix}{\mathrm{10cos}\:\mathrm{135}°}\\{\mathrm{10sin}\:\mathrm{135}°}\end{pmatrix} \\ $$$${P}=\begin{pmatrix}{\mathrm{0}}\\{−\mathrm{9}}\end{pmatrix}\:\:{Q}=\begin{pmatrix}{\mathrm{5}\sqrt{\mathrm{2}}}\\{\mathrm{5}\sqrt{\mathrm{2}}}\end{pmatrix}\:\:{R}=\begin{pmatrix}{−\mathrm{5}\sqrt{\mathrm{2}}}\\{\mathrm{5}\sqrt{\mathrm{2}}}\end{pmatrix} \\ $$$${P}+{Q}+{R}=\begin{pmatrix}{\mathrm{0}}\\{\mathrm{10}\sqrt{\mathrm{2}}−\mathrm{9}}\end{pmatrix} \\ $$
Answered by behi83417@gmail.com last updated on 23/Jun/19
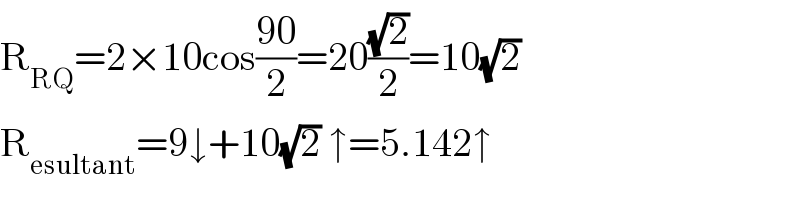
$$\mathrm{R}_{\mathrm{RQ}} =\mathrm{2}×\mathrm{10cos}\frac{\mathrm{90}}{\mathrm{2}}=\mathrm{20}\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}=\mathrm{10}\sqrt{\mathrm{2}} \\ $$$$\mathrm{R}_{\mathrm{esultant}} =\mathrm{9}\downarrow+\mathrm{10}\sqrt{\mathrm{2}}\:\uparrow=\mathrm{5}.\mathrm{142}\uparrow \\ $$
