
Question Number 62611 by hovea cw last updated on 23/Jun/19
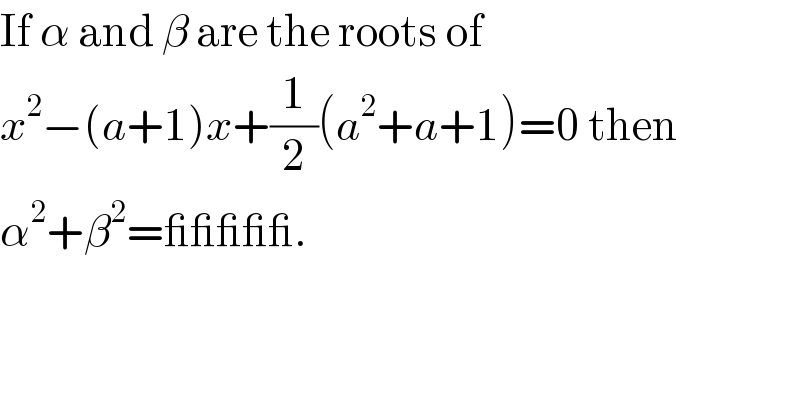
$$\mathrm{If}\:\alpha\:\mathrm{and}\:\beta\:\mathrm{are}\:\mathrm{the}\:\mathrm{roots}\:\mathrm{of} \\ $$$${x}^{\mathrm{2}} −\left({a}+\mathrm{1}\right){x}+\frac{\mathrm{1}}{\mathrm{2}}\left({a}^{\mathrm{2}} +{a}+\mathrm{1}\right)=\mathrm{0}\:\mathrm{then} \\ $$$$\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\_\_\_\_\_. \\ $$
Commented by Prithwish sen last updated on 23/Jun/19
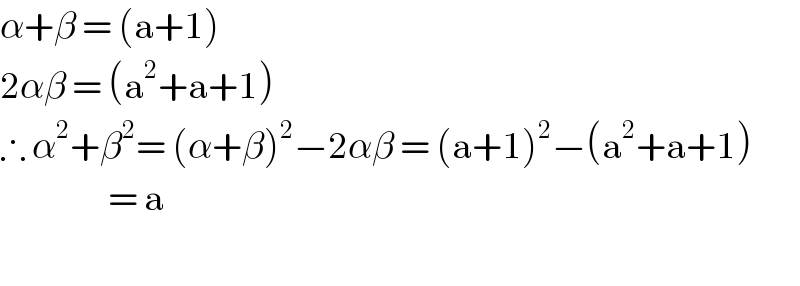
$$\alpha+\beta\:=\:\left(\mathrm{a}+\mathrm{1}\right) \\ $$$$\mathrm{2}\alpha\beta\:=\:\left(\mathrm{a}^{\mathrm{2}} +\mathrm{a}+\mathrm{1}\right)\: \\ $$$$\therefore\:\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\:\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta\:=\:\left(\mathrm{a}+\mathrm{1}\right)^{\mathrm{2}} −\left(\mathrm{a}^{\mathrm{2}} +\mathrm{a}+\mathrm{1}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{a} \\ $$$$\:\:\:\:\:\:\: \\ $$
Commented by mathmax by abdo last updated on 24/Jun/19
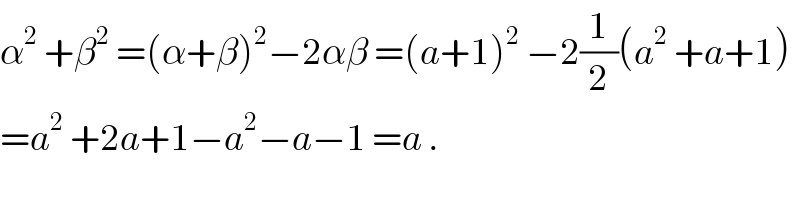
$$\alpha^{\mathrm{2}} \:+\beta^{\mathrm{2}} \:=\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta\:=\left({a}+\mathrm{1}\right)^{\mathrm{2}} \:−\mathrm{2}\frac{\mathrm{1}}{\mathrm{2}}\left({a}^{\mathrm{2}} \:+{a}+\mathrm{1}\right) \\ $$$$={a}^{\mathrm{2}} \:+\mathrm{2}{a}+\mathrm{1}−{a}^{\mathrm{2}} −{a}−\mathrm{1}\:={a}\:. \\ $$
