
Question Number 62415 by mathmax by abdo last updated on 20/Jun/19
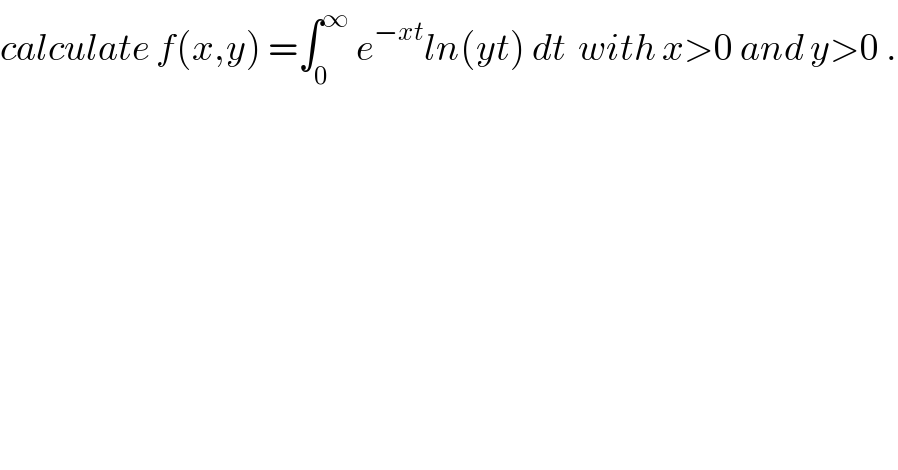
$${calculate}\:{f}\left({x},{y}\right)\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} {ln}\left({yt}\right)\:{dt}\:\:{with}\:{x}>\mathrm{0}\:{and}\:{y}>\mathrm{0}\:. \\ $$
Commented bymathmax by abdo last updated on 23/Jun/19
![we have f(x,y) =∫_0 ^∞ e^(−xt) (lny +ln(t)dt =ln(y)∫_0 ^∞ e^(−xt) dt +∫_0 ^∞ e^(−xt) ln(t)dt ∫_0 ^∞ e^(−xt) dt =[−(1/x)e^(−xt) ]_(t=0) ^∞ =(1/x) ∫_0 ^∞ e^(−xt) ln(t) dt =_(xt =u) ∫_0 ^∞ e^(−u) ln((u/x))(du/x) =(1/x){ ∫_0 ^∞ e^(−u) ln(u)du−ln(x)∫_0 ^∞ e^(−u) du} =(1/x){ −γ −ln(x)×1} =−(1/x){ln(x)+γ) ⇒ f(x,y) =((ln(y))/x) −(1/x){ln(x)+γ} =(1/x)( ln((y/x))−γ) γ is euler constant number.](Q62567.png)
$${we}\:{have}\:{f}\left({x},{y}\right)\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} \:\left({lny}\:+{ln}\left({t}\right){dt}\:={ln}\left({y}\right)\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} \:{dt}\:+\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} {ln}\left({t}\right){dt}\right. \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} \:{dt}\:=\left[−\frac{\mathrm{1}}{{x}}{e}^{−{xt}} \right]_{{t}=\mathrm{0}} ^{\infty} \:=\frac{\mathrm{1}}{{x}} \\ $$ $$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{xt}} {ln}\left({t}\right)\:{dt}\:=_{{xt}\:={u}} \:\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}} {ln}\left(\frac{{u}}{{x}}\right)\frac{{du}}{{x}} \\ $$ $$=\frac{\mathrm{1}}{{x}}\left\{\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}} \:{ln}\left({u}\right){du}−{ln}\left({x}\right)\int_{\mathrm{0}} ^{\infty} \:{e}^{−{u}} \:{du}\right\} \\ $$ $$=\frac{\mathrm{1}}{{x}}\left\{\:−\gamma\:−{ln}\left({x}\right)×\mathrm{1}\right\}\:=−\frac{\mathrm{1}}{{x}}\left\{{ln}\left({x}\right)+\gamma\right)\:\Rightarrow \\ $$ $${f}\left({x},{y}\right)\:=\frac{{ln}\left({y}\right)}{{x}}\:−\frac{\mathrm{1}}{{x}}\left\{{ln}\left({x}\right)+\gamma\right\}\:=\frac{\mathrm{1}}{{x}}\left(\:{ln}\left(\frac{{y}}{{x}}\right)−\gamma\right) \\ $$ $$\gamma\:{is}\:{euler}\:{constant}\:{number}. \\ $$
