
Question Number 99707 by student work last updated on 22/Jun/20

$$\int_{−\infty} ^{\infty} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}=? \\ $$
Commented by student work last updated on 22/Jun/20

$$\mathrm{help}\:\mathrm{me} \\ $$
Answered by smridha last updated on 22/Jun/20

$$\mathrm{2}\int_{\mathrm{0}} ^{\infty} \boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } {x}^{\mathrm{2}.\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \boldsymbol{{dx}} \\ $$$$=\boldsymbol{\Gamma}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\sqrt{\boldsymbol{\pi}} \\ $$
Answered by smridha last updated on 22/Jun/20
![∫_(−∞) ^∞ e^(−x^2 ) dx=? let′s do it another way I=∫_(−∞) ^(+∞) e^(−x^2 ) dx similarly I=∫_(−∞) ^(+∞) e^(−y^2 ) dy so now I^2 =∫_(−∞) ^(+∞) ∫_(−∞) ^(+∞) e^(−(x^2 +y^2 )) dxdy now by transforming to this integral cartesian to plane−polar co−ordinate we get I^2 =∫_0 ^(2𝛑) d𝛉 ∫_0 ^∞ e^(−r^2 ) rdr=2𝛑.(−(1/2))[e^(−r^2 ) ]_0 ^∞ =𝛑 so I=(√𝛑) (consider positive root). this is one of the valuable integral.](Q99711.png)
$$\int_{−\infty} ^{\infty} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}=? \\ $$$$\boldsymbol{{let}}'{s}\:\boldsymbol{{do}}\:\boldsymbol{{it}}\:\boldsymbol{{another}}\:\boldsymbol{{way}} \\ $$$$\boldsymbol{{I}}=\int_{−\infty} ^{+\infty} \boldsymbol{{e}}^{−\boldsymbol{{x}}^{\mathrm{2}} } \boldsymbol{{dx}}\: \\ $$$$\boldsymbol{{similarly}}\:\boldsymbol{{I}}=\int_{−\infty} ^{+\infty} \boldsymbol{{e}}^{−\boldsymbol{{y}}^{\mathrm{2}} } \boldsymbol{{dy}} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{now}}\:\boldsymbol{{I}}^{\mathrm{2}} =\int_{−\infty} ^{+\infty} \int_{−\infty} ^{+\infty} \boldsymbol{{e}}^{−\left({x}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} \right)} \boldsymbol{{dxdy}} \\ $$$$\boldsymbol{{now}}\:\boldsymbol{{by}}\:\boldsymbol{{transforming}}\:\boldsymbol{{to}}\:\boldsymbol{{this}} \\ $$$$\boldsymbol{{integral}}\:\boldsymbol{{c}}{a}\boldsymbol{{rt}}{e}\boldsymbol{{sian}}\:\boldsymbol{{to}}\:\boldsymbol{{plane}}−\boldsymbol{{polar}} \\ $$$$\boldsymbol{{co}}−\boldsymbol{{ordinate}}\:\boldsymbol{{we}}\:\boldsymbol{{get}} \\ $$$$\boldsymbol{{I}}^{\mathrm{2}} =\int_{\mathrm{0}} ^{\mathrm{2}\boldsymbol{\pi}} \boldsymbol{{d}\theta}\:\int_{\mathrm{0}} ^{\infty} {e}^{−\boldsymbol{{r}}^{\mathrm{2}} } \boldsymbol{{rdr}}=\mathrm{2}\boldsymbol{\pi}.\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)\left[\boldsymbol{{e}}^{−\boldsymbol{{r}}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{\infty} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\boldsymbol{\pi} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{I}}=\sqrt{\boldsymbol{\pi}}\:\left(\boldsymbol{{consider}}\:\boldsymbol{{positive}}\:\boldsymbol{{root}}\right). \\ $$$$\:\:\boldsymbol{{this}}\:\boldsymbol{{is}}\:\boldsymbol{{one}}\:\boldsymbol{{of}}\:\boldsymbol{{the}}\:\boldsymbol{{valuable}}\:\boldsymbol{{integral}}. \\ $$
Answered by mathmax by abdo last updated on 23/Jun/20
![A =∫_(−∞) ^(+∞) e^(−x^2 ) dx ⇒A =2 ∫_0 ^∞ e^(−x^2 ) dx let A_n =∫∫_([(1/n),n[^2 ) e^(−x^2 −y^2 ) dxdy we have A_n =∫_((1 )/n) ^(n ) e^(−x^2 ) dx.∫_(1/n) ^n e^(−y^2 ) dy ⇒lim_(n→+∞) A_n =(∫_0 ^∞ e^(−x^2 ) dx)^2 let considere the diffeomorphisme { ((x = r cosθ)),((y =rsinθ)) :} (1/n)≤x <n and (1/n)≤y<n ⇒(2/n^2 )≤x^2 +y^2 <2n^2 ⇒(2/n^2 )≤r^2 <2n^2 ⇒((√2)/n)≤r<n(√2) ⇒A_n =∫∫_(((√2)/n)≤r<n(√2)and 0≤θ≤(π/2)) e^(−r^2 ) rdrdθ =∫_((√2)/n) ^(n(√2)) re^(−r^2 ) dr ∫_0 ^(π/2) dθ =(π/2)[−(1/2)e^(−r^2 ) ]_((√2)/n) ^(n(√2)) =−(π/4){ e^(−2n^2 ) −e^(−(2/n^2 )) } ⇒ lim_(n→+∞) A_n =(π/4) =(∫_0 ^∞ e^(−x^2 ) dx)^2 but ∫_0 ^∞ e^(−x^2 ) dx >0 ⇒ ∫_0 ^∞ e^(−x^2 ) dx =((√π)/2) ⇒★ A =(√π)★](Q99716.png)
$$ \\ $$$$\mathrm{A}\:=\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:\Rightarrow\mathrm{A}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:\:\mathrm{let}\:\:\mathrm{A}_{\mathrm{n}} =\int\int_{\left[\frac{\mathrm{1}}{\mathrm{n}},\mathrm{n}\left[^{\mathrm{2}} \right.\right.} \:\:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} } \mathrm{dxdy} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{A}_{\mathrm{n}} =\int_{\frac{\mathrm{1}\:}{\mathrm{n}}} ^{\mathrm{n}\:} \:\:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}.\int_{\frac{\mathrm{1}}{\mathrm{n}}} ^{\mathrm{n}} \:\mathrm{e}^{−\mathrm{y}^{\mathrm{2}} } \mathrm{dy}\:\Rightarrow\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \mathrm{A}_{\mathrm{n}} =\left(\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\right)^{\mathrm{2}} \\ $$$$\mathrm{let}\:\mathrm{considere}\:\mathrm{the}\:\mathrm{diffeomorphisme}\:\begin{cases}{\mathrm{x}\:=\:\mathrm{r}\:\mathrm{cos}\theta}\\{\mathrm{y}\:=\mathrm{rsin}\theta}\end{cases} \\ $$$$\frac{\mathrm{1}}{\mathrm{n}}\leqslant\mathrm{x}\:<\mathrm{n}\:\mathrm{and}\:\frac{\mathrm{1}}{\mathrm{n}}\leqslant\mathrm{y}<\mathrm{n}\:\Rightarrow\frac{\mathrm{2}}{\mathrm{n}^{\mathrm{2}} }\leqslant\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} <\mathrm{2n}^{\mathrm{2}} \:\Rightarrow\frac{\mathrm{2}}{\mathrm{n}^{\mathrm{2}} }\leqslant\mathrm{r}^{\mathrm{2}} <\mathrm{2n}^{\mathrm{2}} \:\Rightarrow\frac{\sqrt{\mathrm{2}}}{\mathrm{n}}\leqslant\mathrm{r}<\mathrm{n}\sqrt{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{A}_{\mathrm{n}} =\int\int_{\frac{\sqrt{\mathrm{2}}}{\mathrm{n}}\leqslant\mathrm{r}<\mathrm{n}\sqrt{\mathrm{2}}\mathrm{and}\:\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}} \:\:\:\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} } \mathrm{rdrd}\theta \\ $$$$=\int_{\frac{\sqrt{\mathrm{2}}}{\mathrm{n}}} ^{\mathrm{n}\sqrt{\mathrm{2}}} \:\:\mathrm{re}^{−\mathrm{r}^{\mathrm{2}} } \mathrm{dr}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{d}\theta\:\:=\frac{\pi}{\mathrm{2}}\left[−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{e}^{−\mathrm{r}^{\mathrm{2}} } \right]_{\frac{\sqrt{\mathrm{2}}}{\mathrm{n}}} ^{\mathrm{n}\sqrt{\mathrm{2}}} \:=−\frac{\pi}{\mathrm{4}}\left\{\:\mathrm{e}^{−\mathrm{2n}^{\mathrm{2}} } −\mathrm{e}^{−\frac{\mathrm{2}}{\mathrm{n}^{\mathrm{2}} }} \right\}\:\Rightarrow \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow+\infty} \:\mathrm{A}_{\mathrm{n}} =\frac{\pi}{\mathrm{4}}\:=\left(\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\right)^{\mathrm{2}} \:\:\mathrm{but}\:\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:>\mathrm{0}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow\bigstar\:\mathrm{A}\:=\sqrt{\pi}\bigstar \\ $$
Answered by mathmax by abdo last updated on 23/Jun/20
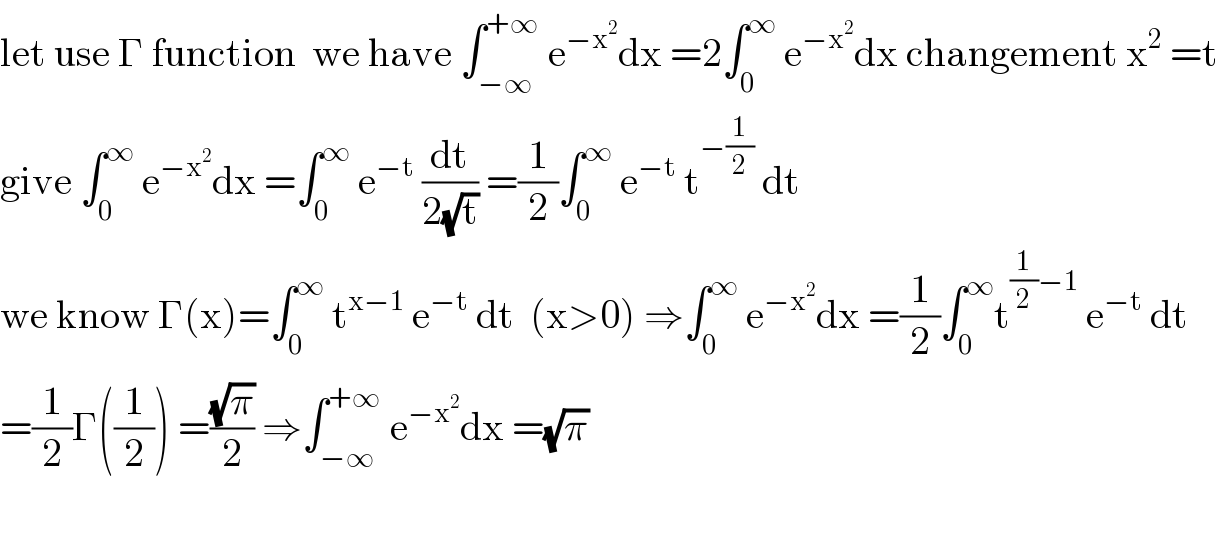
$$\mathrm{let}\:\mathrm{use}\:\Gamma\:\mathrm{function}\:\:\mathrm{we}\:\mathrm{have}\:\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:=\mathrm{2}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:\mathrm{changement}\:\mathrm{x}^{\mathrm{2}} \:=\mathrm{t} \\ $$$$\mathrm{give}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} \:\frac{\mathrm{dt}}{\mathrm{2}\sqrt{\mathrm{t}}}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{dt} \\ $$$$\mathrm{we}\:\mathrm{know}\:\Gamma\left(\mathrm{x}\right)=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{x}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:\:\left(\mathrm{x}>\mathrm{0}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \mathrm{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow\int_{−\infty} ^{+\infty} \:\mathrm{e}^{−\mathrm{x}^{\mathrm{2}} } \mathrm{dx}\:=\sqrt{\pi} \\ $$$$ \\ $$
Commented by student work last updated on 25/Jun/20
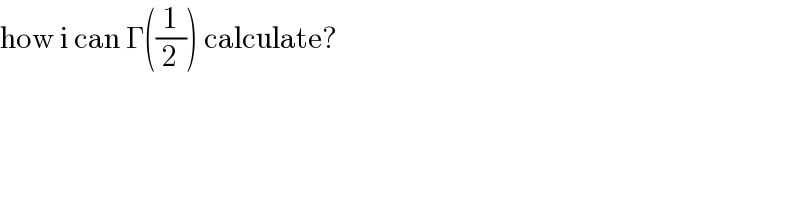
$$\mathrm{how}\:\mathrm{i}\:\mathrm{can}\:\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\mathrm{calculate}? \\ $$
