
Previous in Relation and Functions Next in Relation and Functions
Question Number 62340 by Tawa1 last updated on 19/Jun/19
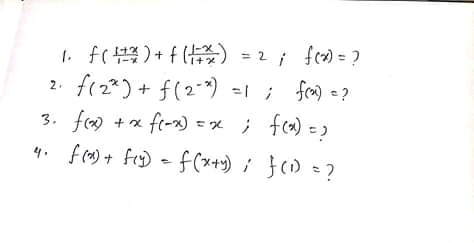
Commented by maxmathsup by imad last updated on 20/Jun/19
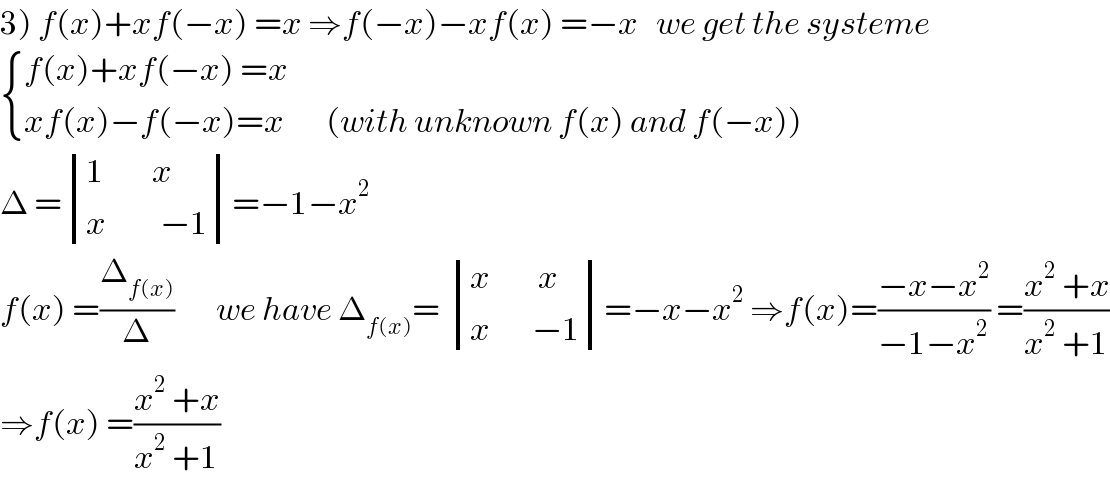
$$\left.\mathrm{3}\right)\:{f}\left({x}\right)+{xf}\left(−{x}\right)\:={x}\:\Rightarrow{f}\left(−{x}\right)−{xf}\left({x}\right)\:=−{x}\:\:\:{we}\:{get}\:{the}\:{systeme} \\ $$$$\begin{cases}{{f}\left({x}\right)+{xf}\left(−{x}\right)\:={x}}\\{{xf}\left({x}\right)−{f}\left(−{x}\right)={x}\:\:\:\:\:\:\:\left({with}\:{unknown}\:{f}\left({x}\right)\:{and}\:{f}\left(−{x}\right)\right)}\end{cases} \\ $$$$\Delta\:=\begin{vmatrix}{\mathrm{1}\:\:\:\:\:\:\:\:{x}}\\{{x}\:\:\:\:\:\:\:\:\:−\mathrm{1}}\end{vmatrix}=−\mathrm{1}−{x}^{\mathrm{2}} \\ $$$${f}\left({x}\right)\:=\frac{\Delta_{{f}\left({x}\right)} }{\Delta}\:\:\:\:\:\:\:{we}\:{have}\:\Delta_{{f}\left({x}\right)} =\:\begin{vmatrix}{{x}\:\:\:\:\:\:\:\:{x}}\\{{x}\:\:\:\:\:\:\:−\mathrm{1}}\end{vmatrix}=−{x}−{x}^{\mathrm{2}} \:\Rightarrow{f}\left({x}\right)=\frac{−{x}−{x}^{\mathrm{2}} }{−\mathrm{1}−{x}^{\mathrm{2}} }\:=\frac{{x}^{\mathrm{2}} \:+{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$\Rightarrow{f}\left({x}\right)\:=\frac{{x}^{\mathrm{2}} \:+{x}}{{x}^{\mathrm{2}} \:+\mathrm{1}} \\ $$
Commented by Tawa1 last updated on 20/Jun/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by prof Abdo imad last updated on 20/Jun/19
$${you}\:{are}\:{welcome}. \\ $$
