
Question Number 62334 by smartsmith459@gmail.com last updated on 19/Jun/19
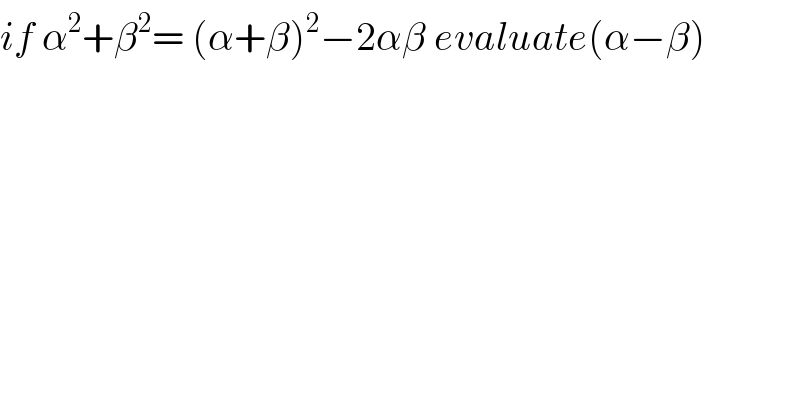
$${if}\:\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\:\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta\:{evaluate}\left(\alpha−\beta\right) \\ $$
Answered by Kunal12588 last updated on 20/Jun/19
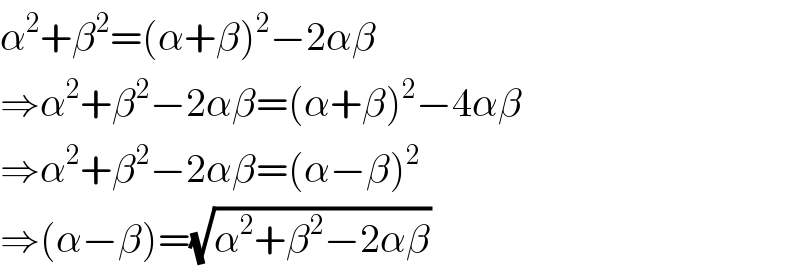
$$\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{2}\alpha\beta \\ $$$$\Rightarrow\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} −\mathrm{2}\alpha\beta=\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{4}\alpha\beta \\ $$$$\Rightarrow\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} −\mathrm{2}\alpha\beta=\left(\alpha−\beta\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left(\alpha−\beta\right)=\sqrt{\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} −\mathrm{2}\alpha\beta} \\ $$
Answered by MJS last updated on 20/Jun/19
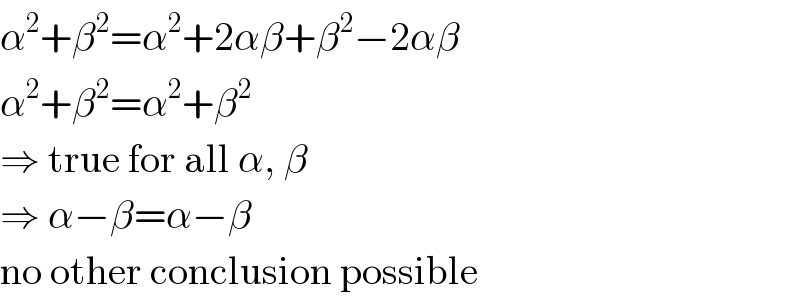
$$\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\alpha^{\mathrm{2}} +\mathrm{2}\alpha\beta+\beta^{\mathrm{2}} −\mathrm{2}\alpha\beta \\ $$$$\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} =\alpha^{\mathrm{2}} +\beta^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:\alpha,\:\beta\: \\ $$$$\Rightarrow\:\alpha−\beta=\alpha−\beta \\ $$$$\mathrm{no}\:\mathrm{other}\:\mathrm{conclusion}\:\mathrm{possible} \\ $$
