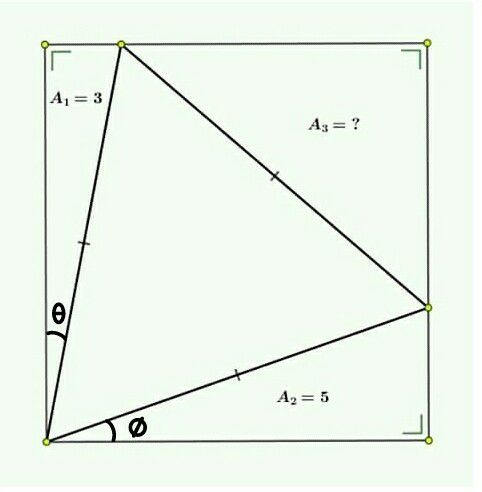
Question Number 62289 by naka3546 last updated on 19/Jun/19
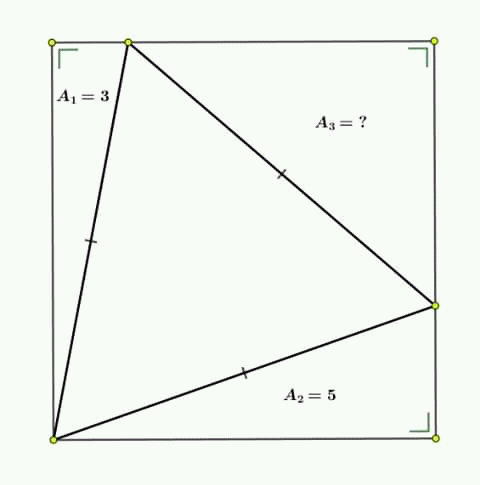
Answered by MJS last updated on 19/Jun/19
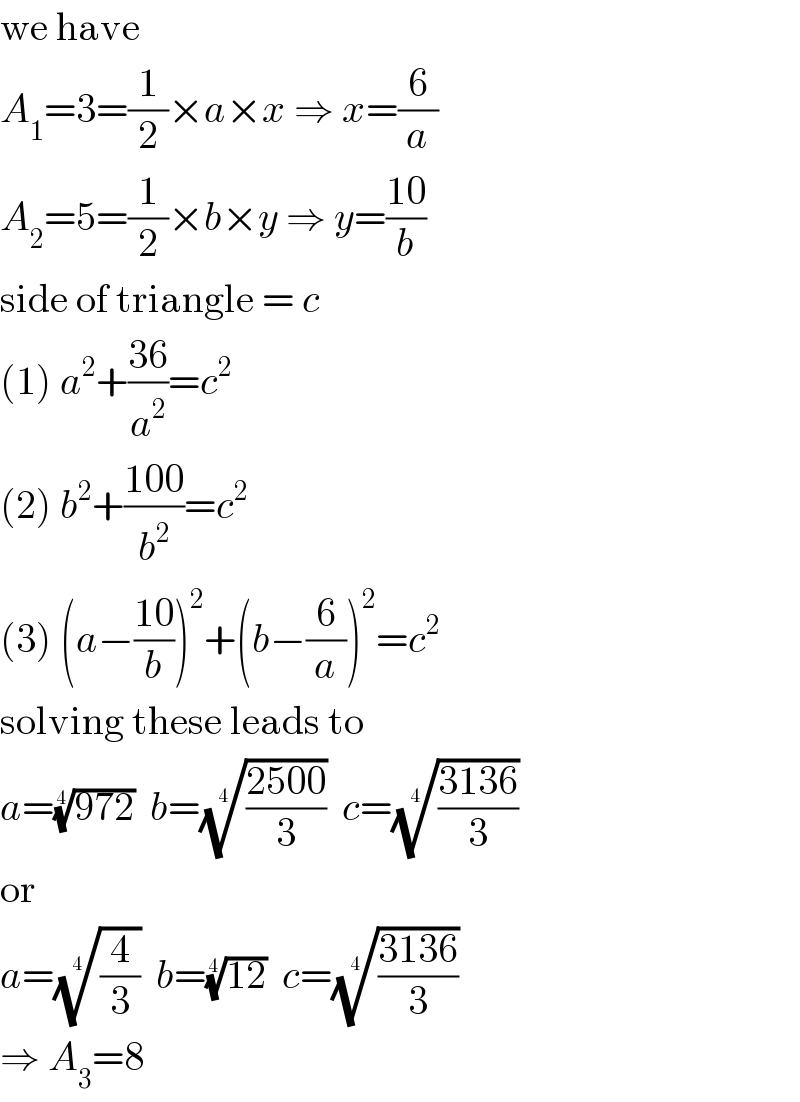
$$\mathrm{we}\:\mathrm{have} \\ $$$${A}_{\mathrm{1}} =\mathrm{3}=\frac{\mathrm{1}}{\mathrm{2}}×{a}×{x}\:\Rightarrow\:{x}=\frac{\mathrm{6}}{{a}} \\ $$$${A}_{\mathrm{2}} =\mathrm{5}=\frac{\mathrm{1}}{\mathrm{2}}×{b}×{y}\:\Rightarrow\:{y}=\frac{\mathrm{10}}{{b}} \\ $$$$\mathrm{side}\:\mathrm{of}\:\mathrm{triangle}\:=\:{c} \\ $$$$\left(\mathrm{1}\right)\:{a}^{\mathrm{2}} +\frac{\mathrm{36}}{{a}^{\mathrm{2}} }={c}^{\mathrm{2}} \\ $$$$\left(\mathrm{2}\right)\:{b}^{\mathrm{2}} +\frac{\mathrm{100}}{{b}^{\mathrm{2}} }={c}^{\mathrm{2}} \\ $$$$\left(\mathrm{3}\right)\:\left({a}−\frac{\mathrm{10}}{{b}}\right)^{\mathrm{2}} +\left({b}−\frac{\mathrm{6}}{{a}}\right)^{\mathrm{2}} ={c}^{\mathrm{2}} \\ $$$$\mathrm{solving}\:\mathrm{these}\:\mathrm{leads}\:\mathrm{to} \\ $$$${a}=\sqrt[{\mathrm{4}}]{\mathrm{972}}\:\:{b}=\sqrt[{\mathrm{4}}]{\frac{\mathrm{2500}}{\mathrm{3}}}\:\:{c}=\sqrt[{\mathrm{4}}]{\frac{\mathrm{3136}}{\mathrm{3}}} \\ $$$$\mathrm{or} \\ $$$${a}=\sqrt[{\mathrm{4}}]{\frac{\mathrm{4}}{\mathrm{3}}}\:\:{b}=\sqrt[{\mathrm{4}}]{\mathrm{12}}\:\:{c}=\sqrt[{\mathrm{4}}]{\frac{\mathrm{3136}}{\mathrm{3}}} \\ $$$$\Rightarrow\:{A}_{\mathrm{3}} =\mathrm{8} \\ $$
Commented by MJS last updated on 19/Jun/19

$$\mathrm{btw}\:\mathrm{only}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{solution}\:\mathrm{looks}\:\mathrm{like}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{picture} \\ $$
Commented by mr W last updated on 19/Jun/19

$${exact}\:{solution},\:{very}\:{nice}\:{sir}! \\ $$$${i}\:{think}\:{A}_{\mathrm{3}} ={A}_{\mathrm{1}} +{A}_{\mathrm{2}} ,\:{proof}\:{see}\:{below}. \\ $$
Answered by mr W last updated on 19/Jun/19
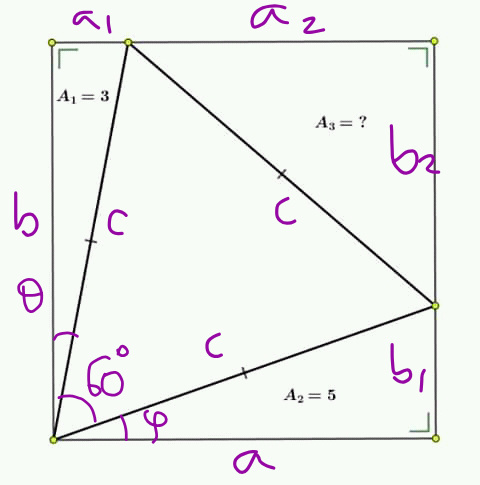
Commented by mr W last updated on 19/Jun/19

$$\varphi=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{3}}−\theta=\frac{\pi}{\mathrm{6}}−\theta \\ $$$$\phi=\pi−\left(\frac{\pi}{\mathrm{2}}−\theta\right)−\frac{\pi}{\mathrm{3}}=\frac{\pi}{\mathrm{6}}+\theta \\ $$$${A}_{\mathrm{1}} =\frac{{c}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{4}} \\ $$$${A}_{\mathrm{2}} =\frac{{c}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\varphi}{\mathrm{4}}=\frac{{c}^{\mathrm{2}} \:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\mathrm{2}\theta\right)}{\mathrm{4}} \\ $$$${A}_{\mathrm{3}} =\frac{{c}^{\mathrm{2}} \:\mathrm{sin}\:\mathrm{2}\phi}{\mathrm{4}}=\frac{{c}^{\mathrm{2}} \:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\mathrm{2}\theta\right)}{\mathrm{4}} \\ $$$$\frac{{A}_{\mathrm{2}} }{{A}_{\mathrm{1}} }=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}−\mathrm{2}\theta\right)}{\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\frac{\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:\mathrm{cos}\:\mathrm{2}\theta−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{sin}\:\mathrm{2}\theta}=\frac{{A}_{\mathrm{2}} }{{A}_{\mathrm{1}} } \\ $$$$\Rightarrow\frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\:\mathrm{2}\theta}=\frac{\mathrm{2}{A}_{\mathrm{2}} }{{A}_{\mathrm{1}} }+\mathrm{1} \\ $$$$\frac{{A}_{\mathrm{3}} }{{A}_{\mathrm{1}} }=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{3}}+\mathrm{2}\theta\right)}{\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{tan}\:\mathrm{2}\theta}+\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}{A}_{\mathrm{2}} }{{A}_{\mathrm{1}} }+\mathrm{1}+\mathrm{1}\right)=\mathrm{1}+\frac{{A}_{\mathrm{2}} }{{A}_{\mathrm{1}} } \\ $$$$\Rightarrow{A}_{\mathrm{3}} ={A}_{\mathrm{1}} \left(\mathrm{1}+\frac{{A}_{\mathrm{2}} }{{A}_{\mathrm{1}} }\right)={A}_{\mathrm{1}} +{A}_{\mathrm{2}} =\mathrm{3}+\mathrm{5}=\mathrm{8} \\ $$
Commented by Tony Lin last updated on 20/Jun/19
![2(A_1 +A_2 )=c^2 sinθcosθ+c^2 sin((π/6)−θ)cos((π/6)−θ) =(1/2)c^2 [sin2θ+sin((π/3)−2θ)] =(1/2)c^2 (((√3)/2)cos2θ+(1/2)sin2θ) =(1/2)c^2 sin((π/3)+2θ) =c^2 cos((π/6)+θ)sin((π/6)+θ) =2A_3](Q62364.png)
$$\mathrm{2}\left({A}_{\mathrm{1}} +{A}_{\mathrm{2}} \right)={c}^{\mathrm{2}} {sin}\theta{cos}\theta+{c}^{\mathrm{2}} {sin}\left(\frac{\pi}{\mathrm{6}}−\theta\right){cos}\left(\frac{\pi}{\mathrm{6}}−\theta\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{c}^{\mathrm{2}} \left[{sin}\mathrm{2}\theta+{sin}\left(\frac{\pi}{\mathrm{3}}−\mathrm{2}\theta\right)\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{c}^{\mathrm{2}} \left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{cos}\mathrm{2}\theta+\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}\theta\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{c}^{\mathrm{2}} {sin}\left(\frac{\pi}{\mathrm{3}}+\mathrm{2}\theta\right) \\ $$$$={c}^{\mathrm{2}} {cos}\left(\frac{\pi}{\mathrm{6}}+\theta\right){sin}\left(\frac{\pi}{\mathrm{6}}+\theta\right) \\ $$$$=\mathrm{2}{A}_{\mathrm{3}} \\ $$
Answered by ajfour last updated on 19/Jun/19
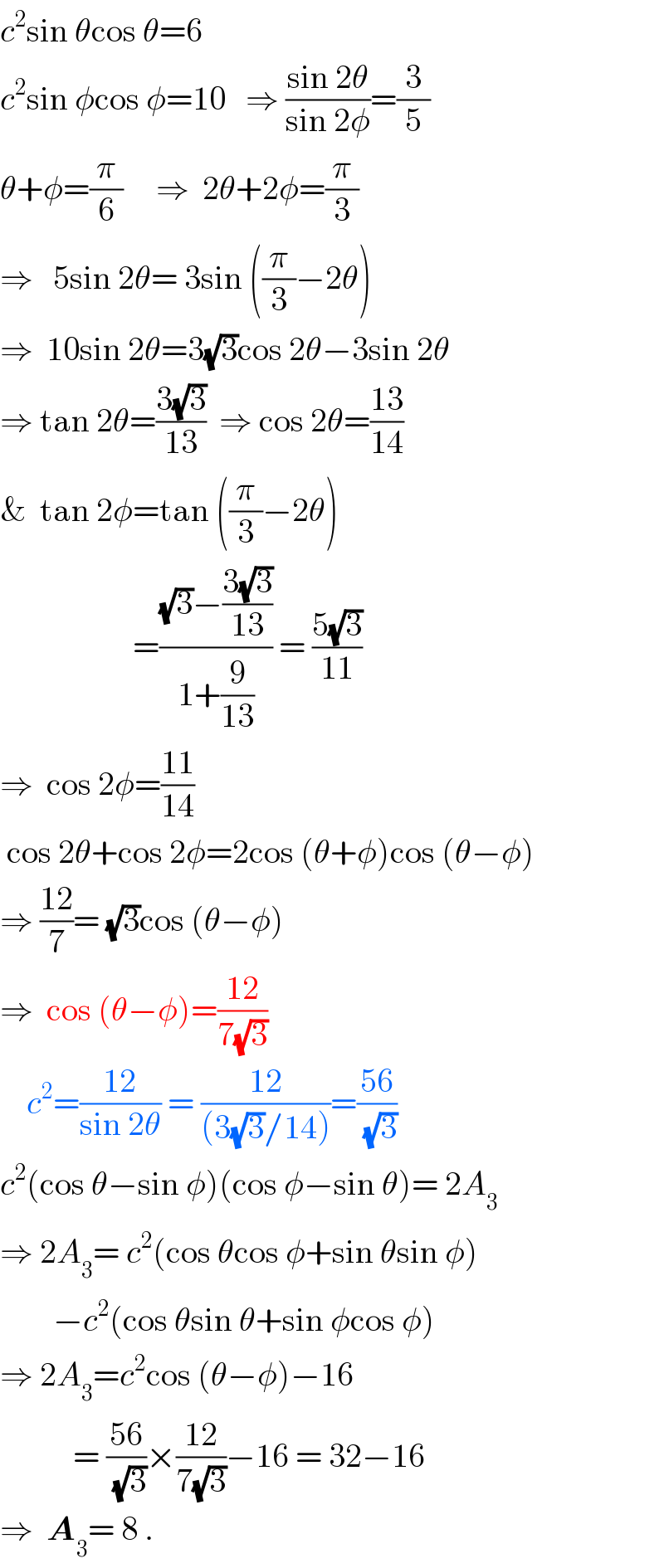
$${c}^{\mathrm{2}} \mathrm{sin}\:\theta\mathrm{cos}\:\theta=\mathrm{6} \\ $$$${c}^{\mathrm{2}} \mathrm{sin}\:\phi\mathrm{cos}\:\phi=\mathrm{10}\:\:\:\Rightarrow\:\frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{sin}\:\mathrm{2}\phi}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$$$\theta+\phi=\frac{\pi}{\mathrm{6}}\:\:\:\:\:\Rightarrow\:\:\mathrm{2}\theta+\mathrm{2}\phi=\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\:\:\:\mathrm{5sin}\:\mathrm{2}\theta=\:\mathrm{3sin}\:\left(\frac{\pi}{\mathrm{3}}−\mathrm{2}\theta\right) \\ $$$$\Rightarrow\:\:\mathrm{10sin}\:\mathrm{2}\theta=\mathrm{3}\sqrt{\mathrm{3}}\mathrm{cos}\:\mathrm{2}\theta−\mathrm{3sin}\:\mathrm{2}\theta \\ $$$$\Rightarrow\:\mathrm{tan}\:\mathrm{2}\theta=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{13}}\:\:\Rightarrow\:\mathrm{cos}\:\mathrm{2}\theta=\frac{\mathrm{13}}{\mathrm{14}} \\ $$$$\&\:\:\mathrm{tan}\:\mathrm{2}\phi=\mathrm{tan}\:\left(\frac{\pi}{\mathrm{3}}−\mathrm{2}\theta\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{3}}−\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{13}}}{\mathrm{1}+\frac{\mathrm{9}}{\mathrm{13}}}\:=\:\frac{\mathrm{5}\sqrt{\mathrm{3}}}{\mathrm{11}} \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\mathrm{2}\phi=\frac{\mathrm{11}}{\mathrm{14}} \\ $$$$\:\mathrm{cos}\:\mathrm{2}\theta+\mathrm{cos}\:\mathrm{2}\phi=\mathrm{2cos}\:\left(\theta+\phi\right)\mathrm{cos}\:\left(\theta−\phi\right) \\ $$$$\Rightarrow\:\frac{\mathrm{12}}{\mathrm{7}}=\:\sqrt{\mathrm{3}}\mathrm{cos}\:\left(\theta−\phi\right) \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\left(\theta−\phi\right)=\frac{\mathrm{12}}{\mathrm{7}\sqrt{\mathrm{3}}} \\ $$$$\:\:\:\:{c}^{\mathrm{2}} =\frac{\mathrm{12}}{\mathrm{sin}\:\mathrm{2}\theta}\:=\:\frac{\mathrm{12}}{\left(\mathrm{3}\sqrt{\mathrm{3}}/\mathrm{14}\right)}=\frac{\mathrm{56}}{\sqrt{\mathrm{3}}} \\ $$$${c}^{\mathrm{2}} \left(\mathrm{cos}\:\theta−\mathrm{sin}\:\phi\right)\left(\mathrm{cos}\:\phi−\mathrm{sin}\:\theta\right)=\:\mathrm{2}{A}_{\mathrm{3}} \\ $$$$\Rightarrow\:\mathrm{2}{A}_{\mathrm{3}} =\:{c}^{\mathrm{2}} \left(\mathrm{cos}\:\theta\mathrm{cos}\:\phi+\mathrm{sin}\:\theta\mathrm{sin}\:\phi\right) \\ $$$$\:\:\:\:\:\:\:\:−{c}^{\mathrm{2}} \left(\mathrm{cos}\:\theta\mathrm{sin}\:\theta+\mathrm{sin}\:\phi\mathrm{cos}\:\phi\right) \\ $$$$\Rightarrow\:\mathrm{2}{A}_{\mathrm{3}} ={c}^{\mathrm{2}} \mathrm{cos}\:\left(\theta−\phi\right)−\mathrm{16} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{56}}{\sqrt{\mathrm{3}}}×\frac{\mathrm{12}}{\mathrm{7}\sqrt{\mathrm{3}}}−\mathrm{16}\:=\:\mathrm{32}−\mathrm{16} \\ $$$$\Rightarrow\:\:\boldsymbol{{A}}_{\mathrm{3}} =\:\mathrm{8}\:. \\ $$
Commented by ajfour last updated on 19/Jun/19