
Question Number 62252 by hovea cw last updated on 18/Jun/19
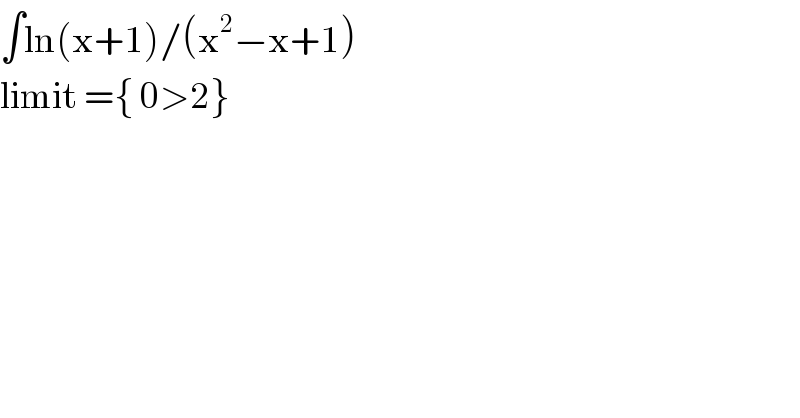
$$\int\mathrm{ln}\left(\mathrm{x}+\mathrm{1}\right)/\left(\mathrm{x}^{\mathrm{2}} −\mathrm{x}+\mathrm{1}\right) \\ $$ $$\mathrm{limit}\:=\left\{\:\mathrm{0}>\mathrm{2}\right\} \\ $$
Commented bymaxmathsup by imad last updated on 18/Jun/19
![let I =∫_0 ^2 ((ln(x+1))/(x^2 −x +1))dx and f(t)=∫_0 ^2 ((ln(1+tx))/(x^2 −x +1)) dx with t≥0 we have I =f(1) and f^′ (t)=∫_0 ^2 (x/((1+tx)(x^2 −x+1)))dx =(1/t)∫_0 ^2 ((1+tx−1)/((1+tx)(x^2 −x+1)))dx =(1/t)∫_0 ^2 (dx/((x^2 −x+1))) −(1/t) ∫_0 ^2 (dx/((tx+1)(x^2 −x+1))) ∫_0 ^2 (dx/(x^2 −x+1)) =∫_0 ^2 (dx/((x−(1/2))^2 +(3/4))) =_(x−(1/2)=((√3)/2)u) (4/3) ∫_(−(1/(√3))) ^(3/(√3)) (1/(u^2 +1)) ((√3)/2)du =(2/(√3)) [arctn(u)]_(−(1/(√3))) ^(√3) =(2/(√3)){ arctan((√3))+arctan((1/(√3)))}=(2/(√3))(π/2) =(π/(√3)) let decompose F(x)=(1/((tx+1)(x^2 −x +1)→(Δ<0))) F(x) =(a/(tx+1)) +((bx+c)/(x^2 −x+1)) a =lim_(x→−(1/t)) (tx+1)F(x) =(t^2 /(t^2 +t+1)) ⇒F(x) =(t^2 /((tx+1)(t^2 +t+1))) +((bx+c)/(x^2 −x +1)) lim_(t→+∞) xF(x) =0 =(a/t) +b ⇒a+tb =0 ⇒tb =−a ⇒b =−(a/t) =−(t/(t^2 +t+1)) ⇒ F(x) =(t^2 /((t^2 +t+1)(tx+1))) +((−(t/(t^2 +t+1))x +c)/(x^2 −x+1)) F(0)=1 =a+c ⇒c =1−a =1−(t^2 /(t^2 +t+1)) =((t+1)/(t^2 +t+1)) ⇒ F(x) =(t^2 /((t^2 +t+1)(tx+1))) −(1/(t^2 +t+1)) ((tx−t−1)/(x^2 −x+1)) ⇒ ∫_0 ^2 F(x)dx =(t^2 /(t^2 +t+1)) ∫_0 ^2 (dx/(tx+1)) −(1/(t^2 +t+1)) ∫_0 ^2 ((tx−t−1)/(x^2 −x +1))dx ∫_0 ^2 (dx/(tx +1)) =(1/t)[ln∣tx+1∣]_0 ^2 =(1/t)ln∣2t+1∣ ∫_0 ^2 ((tx−t−1)/(x^2 −x+1))dx =(t/2)∫_0 ^2 ((2x−1+1)/(x^2 −x+1))dx −(t+1)∫_0 ^2 (dx/(x^2 −x+1)) =(t/2)[ln∣x^2 −x+1∣]_0 ^2 −(t+1)(π/(√3)) =(t/2)ln(3)−(π/(√3))(t+1) ⇒ ∫_0 ^2 F(x)dx =(t/(t^2 +t +1))ln∣2t+1∣ −(1/(t^2 +t+1)){(((ln(3))/2)−(π/(√3)))t−(π/(√3))} ⇒ f^′ (t) =(π/(t(√3))) −(1/t)∫_0 ^2 F(x)dx =(π/(t(√3))) −((ln∣2t+1∣)/(t^(2 ) +t +1)) −((((ln(3))/2)−(π/(√3)))/(t^2 +t +1)) +(π/(t(√3)(t^2 +t +1))) ⇒ f(t) =(π/(√3))ln(t)−∫ ((ln(2t+1))/(t^2 +t +1))dt −(((ln3)/2)−(π/(√3)))∫ (dt/(t^2 +t +1)) +(π/(√3)) ∫ (dt/(t(t^2 +t +1))) +c ...be continued...](Q62260.png)
$${let}\:{I}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\frac{{ln}\left({x}+\mathrm{1}\right)}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}{dx}\:\:\:\:{and}\:\:{f}\left({t}\right)=\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\frac{{ln}\left(\mathrm{1}+{tx}\right)}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}\:{dx}\:\:{with}\:{t}\geqslant\mathrm{0} \\ $$ $${we}\:{have}\:{I}\:={f}\left(\mathrm{1}\right)\:\:\:\:\:\:\:{and}\:{f}^{'} \left({t}\right)=\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\frac{{x}}{\left(\mathrm{1}+{tx}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{dx} \\ $$ $$=\frac{\mathrm{1}}{{t}}\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{\mathrm{1}+{tx}−\mathrm{1}}{\left(\mathrm{1}+{tx}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{dx}\:=\frac{\mathrm{1}}{{t}}\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{{t}}\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\:\:\frac{{dx}}{\left({tx}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)} \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:=\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\frac{{dx}}{\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{3}}{\mathrm{4}}}\:=_{{x}−\frac{\mathrm{1}}{\mathrm{2}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{u}} \:\:\frac{\mathrm{4}}{\mathrm{3}}\:\:\:\:\int_{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{3}}{\sqrt{\mathrm{3}}}} \:\:\:\:\:\frac{\mathrm{1}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}{du} \\ $$ $$=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\:\left[{arctn}\left({u}\right)\right]_{−\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}} ^{\sqrt{\mathrm{3}}} \:\:\:=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\left\{\:{arctan}\left(\sqrt{\mathrm{3}}\right)+{arctan}\left(\frac{\mathrm{1}}{\sqrt{\mathrm{3}}}\right)\right\}=\frac{\mathrm{2}}{\sqrt{\mathrm{3}}}\frac{\pi}{\mathrm{2}}\:=\frac{\pi}{\sqrt{\mathrm{3}}} \\ $$ $${let}\:{decompose}\:{F}\left({x}\right)=\frac{\mathrm{1}}{\left({tx}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}\:+\mathrm{1}\right)\rightarrow\left(\Delta<\mathrm{0}\right)} \\ $$ $${F}\left({x}\right)\:=\frac{{a}}{{tx}+\mathrm{1}}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$ $${a}\:={lim}_{{x}\rightarrow−\frac{\mathrm{1}}{{t}}} \:\:\:\left({tx}+\mathrm{1}\right){F}\left({x}\right)\:=\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}}\:\Rightarrow{F}\left({x}\right)\:=\frac{{t}^{\mathrm{2}} }{\left({tx}+\mathrm{1}\right)\left({t}^{\mathrm{2}} \:+{t}+\mathrm{1}\right)}\:+\frac{{bx}+{c}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}} \\ $$ $${lim}_{{t}\rightarrow+\infty} \:{xF}\left({x}\right)\:=\mathrm{0}\:=\frac{{a}}{{t}}\:+{b}\:\Rightarrow{a}+{tb}\:=\mathrm{0}\:\Rightarrow{tb}\:=−{a}\:\Rightarrow{b}\:=−\frac{{a}}{{t}}\:=−\frac{{t}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}}\:\Rightarrow \\ $$ $${F}\left({x}\right)\:=\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)\left({tx}+\mathrm{1}\right)}\:+\frac{−\frac{{t}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}{x}\:+{c}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$ $${F}\left(\mathrm{0}\right)=\mathrm{1}\:={a}+{c}\:\Rightarrow{c}\:=\mathrm{1}−{a}\:=\mathrm{1}−\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:=\frac{{t}+\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:\Rightarrow \\ $$ $${F}\left({x}\right)\:=\frac{{t}^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +{t}+\mathrm{1}\right)\left({tx}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:\frac{{tx}−{t}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}\:\Rightarrow \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{2}} {F}\left({x}\right){dx}\:=\frac{{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +{t}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\frac{{dx}}{{tx}+\mathrm{1}}\:−\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\:\frac{{tx}−{t}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}\:+\mathrm{1}}{dx} \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\frac{{dx}}{{tx}\:+\mathrm{1}}\:=\frac{\mathrm{1}}{{t}}\left[{ln}\mid{tx}+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\mathrm{2}} \:=\frac{\mathrm{1}}{{t}}{ln}\mid\mathrm{2}{t}+\mathrm{1}\mid \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{{tx}−{t}−\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}\:=\frac{{t}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{2}} \:\:\frac{\mathrm{2}{x}−\mathrm{1}+\mathrm{1}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{dx}\:−\left({t}+\mathrm{1}\right)\int_{\mathrm{0}} ^{\mathrm{2}} \:\frac{{dx}}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$ $$=\frac{{t}}{\mathrm{2}}\left[{ln}\mid{x}^{\mathrm{2}} −{x}+\mathrm{1}\mid\right]_{\mathrm{0}} ^{\mathrm{2}} \:−\left({t}+\mathrm{1}\right)\frac{\pi}{\sqrt{\mathrm{3}}}\:=\frac{{t}}{\mathrm{2}}{ln}\left(\mathrm{3}\right)−\frac{\pi}{\sqrt{\mathrm{3}}}\left({t}+\mathrm{1}\right)\:\Rightarrow \\ $$ $$\int_{\mathrm{0}} ^{\mathrm{2}} \:{F}\left({x}\right){dx}\:=\frac{{t}}{{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}{ln}\mid\mathrm{2}{t}+\mathrm{1}\mid\:−\frac{\mathrm{1}}{{t}^{\mathrm{2}} \:+{t}+\mathrm{1}}\left\{\left(\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{2}}−\frac{\pi}{\sqrt{\mathrm{3}}}\right){t}−\frac{\pi}{\sqrt{\mathrm{3}}}\right\}\:\Rightarrow \\ $$ $${f}^{'} \left({t}\right)\:=\frac{\pi}{{t}\sqrt{\mathrm{3}}}\:−\frac{\mathrm{1}}{{t}}\int_{\mathrm{0}} ^{\mathrm{2}} {F}\left({x}\right){dx} \\ $$ $$=\frac{\pi}{{t}\sqrt{\mathrm{3}}}\:−\frac{{ln}\mid\mathrm{2}{t}+\mathrm{1}\mid}{{t}^{\mathrm{2}\:} \:\:+{t}\:+\mathrm{1}}\:−\frac{\frac{{ln}\left(\mathrm{3}\right)}{\mathrm{2}}−\frac{\pi}{\sqrt{\mathrm{3}}}}{{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}\:+\frac{\pi}{{t}\sqrt{\mathrm{3}}\left({t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}\right)}\:\Rightarrow \\ $$ $${f}\left({t}\right)\:=\frac{\pi}{\sqrt{\mathrm{3}}}{ln}\left({t}\right)−\int\:\:\frac{{ln}\left(\mathrm{2}{t}+\mathrm{1}\right)}{{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}{dt}\:−\left(\frac{{ln}\mathrm{3}}{\mathrm{2}}−\frac{\pi}{\sqrt{\mathrm{3}}}\right)\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}}\:+\frac{\pi}{\sqrt{\mathrm{3}}}\:\int\:\:\:\frac{{dt}}{{t}\left({t}^{\mathrm{2}} \:+{t}\:+\mathrm{1}\right)}\:+{c} \\ $$ $$...{be}\:{continued}... \\ $$ $$ \\ $$ $$ \\ $$
