
Question Number 62227 by behi83417@gmail.com last updated on 17/Jun/19
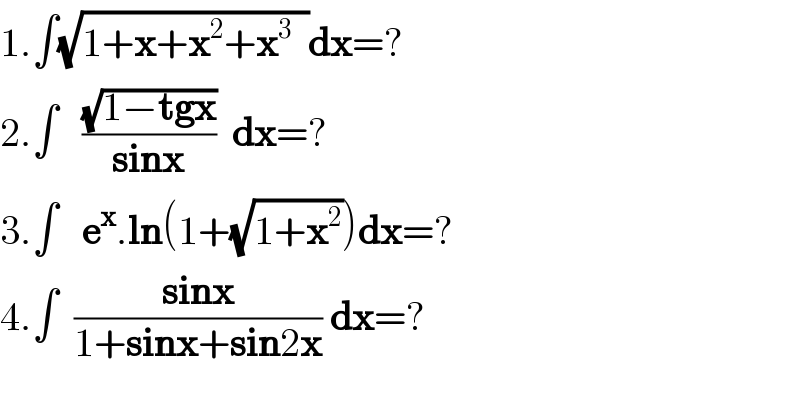
$$\mathrm{1}.\int\sqrt{\mathrm{1}+\boldsymbol{\mathrm{x}}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} +\boldsymbol{\mathrm{x}}^{\mathrm{3}} \:\:}\boldsymbol{\mathrm{dx}}=? \\ $$$$\mathrm{2}.\int\:\:\:\frac{\sqrt{\mathrm{1}−\boldsymbol{\mathrm{tgx}}}}{\boldsymbol{\mathrm{sinx}}}\:\:\boldsymbol{\mathrm{dx}}=? \\ $$$$\mathrm{3}.\int\:\:\:\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} .\boldsymbol{\mathrm{ln}}\left(\mathrm{1}+\sqrt{\mathrm{1}+\boldsymbol{\mathrm{x}}^{\mathrm{2}} }\right)\boldsymbol{\mathrm{dx}}=? \\ $$$$\mathrm{4}.\int\:\:\frac{\boldsymbol{\mathrm{sinx}}}{\mathrm{1}+\boldsymbol{\mathrm{sinx}}+\boldsymbol{\mathrm{sin}}\mathrm{2}\boldsymbol{\mathrm{x}}}\:\boldsymbol{\mathrm{dx}}=? \\ $$
Commented by maxmathsup by imad last updated on 19/Jun/19

$$\left.\mathrm{4}\right)\:{let}\:{I}\:=\int\:\:\:\frac{{sinx}}{\mathrm{1}+{sinx}\:+{sin}\left(\mathrm{2}{x}\right)}{dx}\:\Rightarrow{I}\:=\:\int\:\:\:\:\frac{{sinx}}{\mathrm{1}+{sinx}\:+\mathrm{2}{sinx}\:{cosx}}{dx} \\ $$$$=\:\int\:\:\:\:\:\:\frac{{dx}}{\frac{\mathrm{1}}{{sinx}}+\mathrm{1}\:+\mathrm{2}{cosx}}\:{dx}\:=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}} \:\:\:\:\:\:\int\:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}+{t}^{\mathrm{2}} }{\mathrm{2}{t}}\:+\mathrm{1}+\mathrm{2}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\:\:\:\frac{\mathrm{2}{dt}}{\frac{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{2}{t}}\:+\mathrm{1}+{t}^{\mathrm{2}} \:+\mathrm{2}−\mathrm{2}{t}^{\mathrm{2}} }\:{dt}\:=\int\:\:\:\frac{\mathrm{2}{dt}}{\frac{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{\mathrm{2}{t}}\:+\mathrm{3}−{t}^{\mathrm{2}} } \\ $$$$=\:\int\:\:\:\:\frac{\mathrm{4}{t}\:{dt}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} \:+\mathrm{6}{t}−\mathrm{2}{t}^{\mathrm{3}} }\:=\:\int\:\:\:\frac{\mathrm{4}{tdt}}{{t}^{\mathrm{4}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{1}+\mathrm{6}{t}−\mathrm{2}{t}^{\mathrm{3}} } \\ $$$$=\int\:\:\:\frac{\mathrm{4}{tdt}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{6}{t}+\mathrm{1}}\:\:{let}\:{decompose}\:{F}\left({t}\right)\:=\frac{\mathrm{4}{t}}{{t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{6}{t}\:+\mathrm{1}} \\ $$$${the}\:{roots}\:{of}\:{P}\left({x}\right)\:={t}^{\mathrm{4}} −\mathrm{2}{t}^{\mathrm{3}} \:+\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{6}{t}\:+\mathrm{1}\:{are}\:{t}_{\mathrm{1}} =−\mathrm{1}\:\:,{t}_{\mathrm{2}} \sim−\mathrm{0},\mathrm{1795} \\ $$$${t}_{\mathrm{3}} \sim\mathrm{1},\mathrm{5898}\:+\mathrm{1},\mathrm{7445}{i}\:\:\left({complex}\right) \\ $$$${t}_{\mathrm{4}} \sim\:\mathrm{1},\mathrm{5898}+\mathrm{1},\mathrm{7445}{i}\:\left({complex}\right)\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\frac{\mathrm{4}{t}}{\left({t}+\mathrm{1}\right)\left({t}−{t}_{\mathrm{2}} \right)\left({t}−{t}_{\mathrm{3}} \right)\left({t}−\overset{−} {{t}}_{\mathrm{3}} \right)}\:=\frac{\mathrm{4}{t}}{\left({t}+\mathrm{1}\right)\left({t}−{t}_{\mathrm{2}} \right)\left({t}^{\mathrm{2}} −\left({t}_{\mathrm{3}} +\overset{−} {{t}}_{\mathrm{3}} \right){t}\:+\mid{t}_{\mathrm{3}} \mid^{\mathrm{2}} \right)} \\ $$$$\Rightarrow{F}\left({t}\right)\:=\frac{{a}}{{t}+\mathrm{1}}\:+\frac{{b}}{{t}−{t}_{\mathrm{2}} }\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} −\alpha{t}\:+\beta}\:\:\:\:\:\:\:\:\left(\alpha\:={t}_{\mathrm{3}} +\overset{−} {{t}}_{\mathrm{3}} \:\:{and}\:\beta\:=\mid{t}_{\mathrm{3}} \mid^{\mathrm{2}} \right)\:\Rightarrow \\ $$$$\int\:{F}\left({t}\right){dt}\:={aln}\mid{t}+\mathrm{1}\mid\:+{bln}\mid{t}−{t}_{\mathrm{2}} \mid\:\:+\frac{{c}}{\mathrm{2}}\:\int\:\:\frac{\mathrm{2}{t}−\alpha\:+\alpha}{{t}^{\mathrm{2}} −\alpha{t}\:+\beta}\:+\:\int\:\:\frac{{d}}{{t}^{\mathrm{2}} −\alpha{t}\:+\beta}\:{dt} \\ $$$$={aln}\mid{t}+\mathrm{1}\mid\:+{bln}\mid{t}−{t}_{\mathrm{2}} \mid\:+\frac{{c}}{\mathrm{2}}{ln}\mid{t}^{\mathrm{2}} −\alpha{t}\:+\beta\mid\:\:+\left(\frac{\alpha{c}}{\mathrm{2}}\:+{d}\right)\:\int\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} −\alpha{t}\:+\beta} \\ $$$$\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} −\alpha{t}\:+\beta}\:=\int\:\:\:\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{2}{t}\frac{\alpha}{\mathrm{2}}\:+\beta\:−\frac{\alpha^{\mathrm{2}} }{\mathrm{4}}}\:=\int\:\:\:\:\:\frac{{dt}}{\left({t}−\frac{\alpha}{\mathrm{2}}\right)^{\mathrm{2}} \:+\frac{\mathrm{4}\beta−\alpha^{\mathrm{2}} }{\mathrm{4}}} \\ $$$$=_{{t}−\frac{\alpha}{\mathrm{2}}=\frac{\sqrt{\mathrm{4}\beta−\alpha^{\mathrm{2}} }}{\mathrm{2}}\:{u}} \:\:\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\:\:\:\:\frac{\mathrm{1}}{\frac{\mathrm{4}\beta−\alpha^{\mathrm{2}} }{\mathrm{4}}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:\sqrt{\mathrm{4}\beta−\alpha^{\mathrm{2}} }{du}\:=\frac{\mathrm{2}}{\sqrt{\mathrm{4}\beta−\alpha^{\mathrm{2}} }}\:{arctan}\left({u}\right)\:\:+{C} \\ $$$$=\frac{\mathrm{2}}{\sqrt{\mathrm{4}\beta−\alpha^{\mathrm{2}} }}\:{arctan}\left(\frac{\mathrm{2}{t}−\alpha}{\sqrt{\mathrm{4}\beta^{\mathrm{2}} −\alpha^{\mathrm{2}} }}\right)\:\Rightarrow \\ $$$${I}\:={a}\:{ln}\mid\mathrm{1}+{tan}\left(\frac{{x}}{\mathrm{2}}\right)\mid+{bln}\mid{tan}\left(\frac{{x}}{\mathrm{2}}\right)−{t}_{\mathrm{2}} \mid\:+\frac{{c}}{\mathrm{2}}{ln}\mid{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)−\alpha{tan}\left(\frac{{x}}{\mathrm{2}}\right)+\beta\mid \\ $$$$+\left(\frac{\alpha{c}}{\mathrm{2}}\:+{d}\right)\:\frac{\mathrm{2}}{\sqrt{\mathrm{4}\beta−\alpha^{\mathrm{2}} }}\:{arctan}\left(\frac{\mathrm{2}{tan}\left(\frac{{x}}{\mathrm{2}}\right)}{\sqrt{\mathrm{4}\beta−\alpha^{\mathrm{2}} }}\right)\:+{C}\:\:{rest}\:{to}\:{calculate}\:{the}\:{value}\:{of} \\ $$$${a}\:,{b},{c}\:{and}\:{d}\:.... \\ $$
Commented by behi83417@gmail.com last updated on 20/Jun/19

$$\mathrm{thanks}\:\mathrm{in}\:\mathrm{advance}\:\mathrm{master}\:\mathrm{proph}.\:\mathrm{abdo}! \\ $$$$\mathrm{nice}\:\mathrm{and}\:\mathrm{hard}\:\mathrm{work}. \\ $$
Commented by prof Abdo imad last updated on 20/Jun/19
$${you}\:{are}\:{welcome}\:{sir}. \\ $$
