
Question Number 62201 by maxmathsup by imad last updated on 17/Jun/19
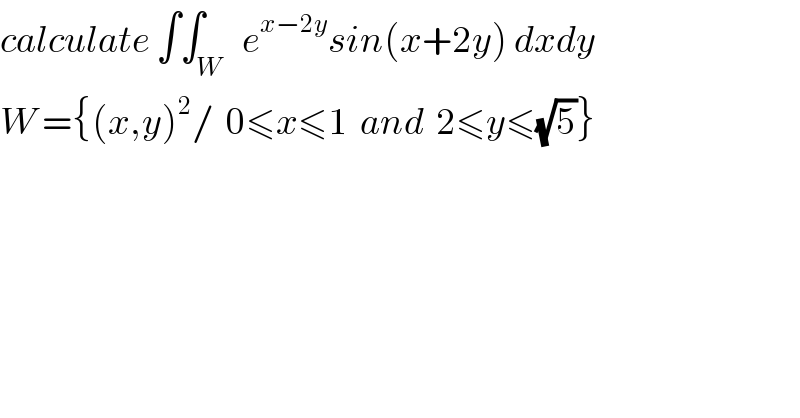
$${calculate}\:\int\int_{{W}} \:\:{e}^{{x}−\mathrm{2}{y}} {sin}\left({x}+\mathrm{2}{y}\right)\:{dxdy} \\ $$$${W}\:=\left\{\left({x},{y}\right)^{\mathrm{2}} /\:\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:\:{and}\:\:\mathrm{2}\leqslant{y}\leqslant\sqrt{\mathrm{5}}\right\} \\ $$
Commented by mathmax by abdo last updated on 04/Jul/19

$${let}\:{use}\:{the}\:{diffeomorphism}\:\left({u},{v}\right)\rightarrow\varphi\left({u},{v}\right)=\left({x},{y}\right)\:/{x}−\mathrm{2}{y}\:={u}\:{and}\:{x}+\mathrm{2}{y}\:={v}\:\Rightarrow \\ $$$${x}\:=\frac{{u}+{v}}{\mathrm{2}}\:{and}\:\:{y}\:=\frac{−{u}+{v}}{\mathrm{4}}\:\Rightarrow\varphi_{\mathrm{1}} \left({u},{v}\right)=\frac{{u}+{v}}{\mathrm{2}}\:{and}\:\varphi_{\mathrm{2}} \left({u},{v}\right)=\frac{−{u}+{v}}{\mathrm{4}} \\ $$$$\:{we}\:{have}\:\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:{and}\:\:−\mathrm{2}\sqrt{\mathrm{5}}\leqslant−\mathrm{2}{y}\leqslant−\mathrm{4}\:\Rightarrow−\mathrm{2}\sqrt{\mathrm{5}}\leqslant{x}−\mathrm{2}{y}\leqslant−\mathrm{3}\:\Rightarrow−\mathrm{2}\sqrt{\mathrm{5}}\leqslant{u}\leqslant−\mathrm{3} \\ $$$$\mathrm{4}\leqslant\mathrm{2}{y}\leqslant\mathrm{2}\sqrt{\mathrm{5}}\:\Rightarrow\:\mathrm{4}\leqslant{x}+\mathrm{2}{y}\leqslant\:\mathrm{1}+\mathrm{2}\sqrt{\mathrm{5}}\:\Rightarrow\:\mathrm{4}\leqslant{v}\leqslant\mathrm{1}+\mathrm{2}\sqrt{\mathrm{5}} \\ $$$$\int\int_{{W}} \:\:\:{f}\left({x},{ydxdy}\:=\int\int_{{w}} {fo}\varphi\left({u},{v}\right)\mid{j}_{\varphi} \mid\:{du}\:{dv}\right. \\ $$$${M}_{{j}} \left(\varphi\right)\:=\begin{pmatrix}{\frac{\partial\varphi_{\mathrm{1}} }{\partial{u}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\partial\varphi_{\mathrm{1}} }{\partial{v}}}\\{\frac{\partial\varphi_{\mathrm{2}} }{\partial{u}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\partial\varphi_{\mathrm{2}} }{\partial{v}}}\end{pmatrix}\:\:\:\:\:\:=\:\begin{pmatrix}{\frac{\mathrm{1}}{\mathrm{2}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}}\\{−\frac{\mathrm{1}}{\mathrm{4}}\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{4}}}\end{pmatrix} \\ $$$${det}\:{Mj}\left(\varphi\right)\:=\frac{\mathrm{2}}{\mathrm{8}}\:=\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow \\ $$$${I}\:=\int\int_{−\mathrm{2}\sqrt{\mathrm{5}}\leqslant{u}\leqslant−\mathrm{3}\:{and}\:\:\mathrm{4}\leqslant{v}\leqslant\mathrm{1}+\mathrm{2}\sqrt{\mathrm{5}}} \:\:\:\:\:{e}^{{u}} {sin}\left({v}\right)\:\frac{\mathrm{1}}{\mathrm{4}}\:{du}\:{dv} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{−\mathrm{2}\sqrt{\mathrm{5}}} ^{−\mathrm{3}} \:{e}^{{u}} {du}\:.\:\int_{\mathrm{4}} ^{\mathrm{1}+\mathrm{2}\sqrt{\mathrm{5}}} \:\:\:{sin}\left({v}\right){dv} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\:{e}^{−\mathrm{3}} \:−{e}^{−\mathrm{2}\sqrt{\mathrm{5}}} \right)\left(\:\:{cos}\left(\mathrm{4}\right)−{cos}\left(\mathrm{1}+\mathrm{2}\sqrt{\mathrm{5}}\right)\right)\:. \\ $$
