
Question Number 619 by Cheenz last updated on 11/Feb/15
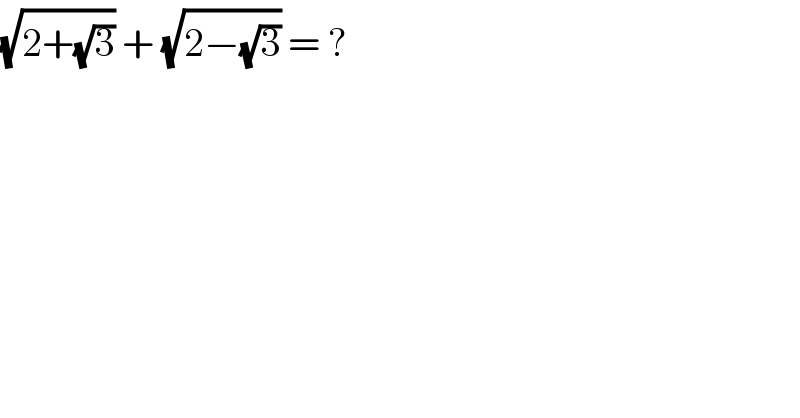
$$\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:+\:\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\:=\:? \\ $$
Answered by 123456 last updated on 11/Feb/15
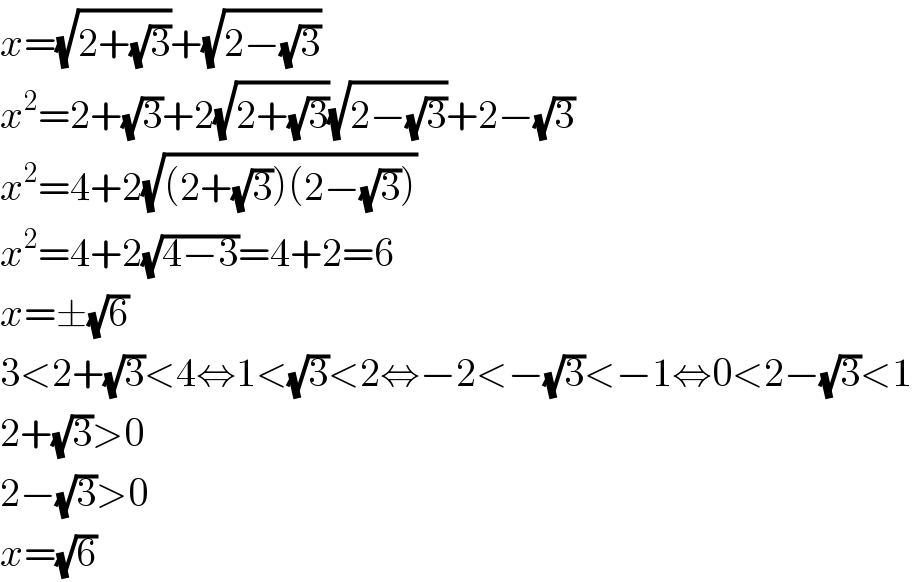
$${x}=\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}+\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$${x}^{\mathrm{2}} =\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{2}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}+\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$${x}^{\mathrm{2}} =\mathrm{4}+\mathrm{2}\sqrt{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)} \\ $$$${x}^{\mathrm{2}} =\mathrm{4}+\mathrm{2}\sqrt{\mathrm{4}−\mathrm{3}}=\mathrm{4}+\mathrm{2}=\mathrm{6} \\ $$$${x}=\pm\sqrt{\mathrm{6}} \\ $$$$\mathrm{3}<\mathrm{2}+\sqrt{\mathrm{3}}<\mathrm{4}\Leftrightarrow\mathrm{1}<\sqrt{\mathrm{3}}<\mathrm{2}\Leftrightarrow−\mathrm{2}<−\sqrt{\mathrm{3}}<−\mathrm{1}\Leftrightarrow\mathrm{0}<\mathrm{2}−\sqrt{\mathrm{3}}<\mathrm{1} \\ $$$$\mathrm{2}+\sqrt{\mathrm{3}}>\mathrm{0} \\ $$$$\mathrm{2}−\sqrt{\mathrm{3}}>\mathrm{0} \\ $$$${x}=\sqrt{\mathrm{6}} \\ $$
Commented by 123456 last updated on 11/Feb/15
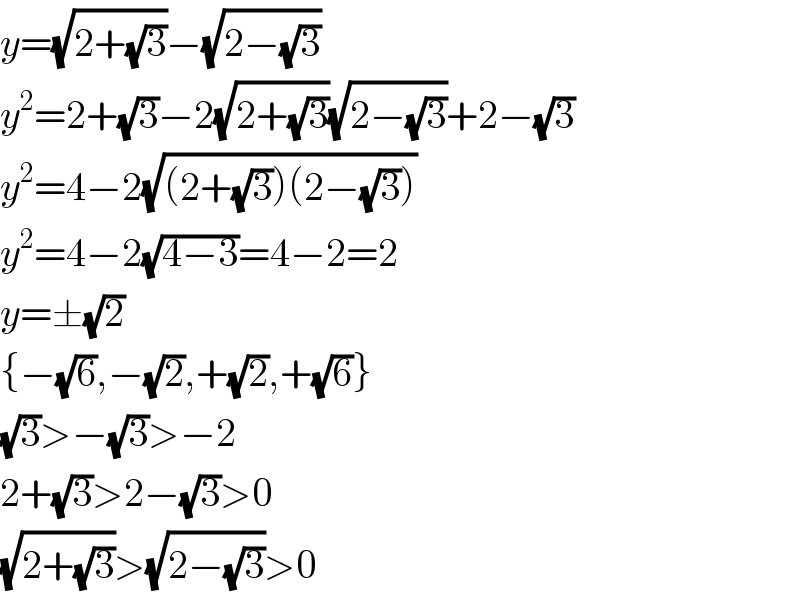
$${y}=\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}−\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$${y}^{\mathrm{2}} =\mathrm{2}+\sqrt{\mathrm{3}}−\mathrm{2}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}+\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$${y}^{\mathrm{2}} =\mathrm{4}−\mathrm{2}\sqrt{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)} \\ $$$${y}^{\mathrm{2}} =\mathrm{4}−\mathrm{2}\sqrt{\mathrm{4}−\mathrm{3}}=\mathrm{4}−\mathrm{2}=\mathrm{2} \\ $$$${y}=\pm\sqrt{\mathrm{2}} \\ $$$$\left\{−\sqrt{\mathrm{6}},−\sqrt{\mathrm{2}},+\sqrt{\mathrm{2}},+\sqrt{\mathrm{6}}\right\} \\ $$$$\sqrt{\mathrm{3}}>−\sqrt{\mathrm{3}}>−\mathrm{2} \\ $$$$\mathrm{2}+\sqrt{\mathrm{3}}>\mathrm{2}−\sqrt{\mathrm{3}}>\mathrm{0} \\ $$$$\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}>\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}>\mathrm{0} \\ $$
