
Question Number 61322 by Tawa1 last updated on 31/May/19

Answered by MJS last updated on 02/Jun/19
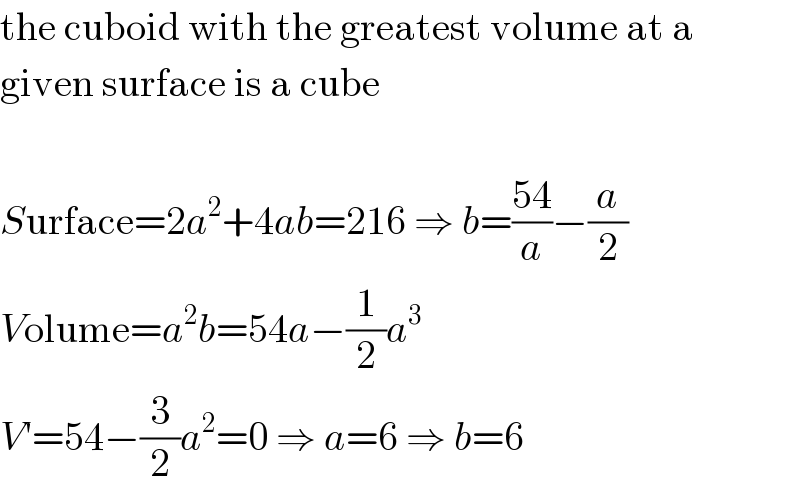
$$\mathrm{the}\:\mathrm{cuboid}\:\mathrm{with}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{volume}\:\mathrm{at}\:\mathrm{a} \\ $$$$\mathrm{given}\:\mathrm{surface}\:\mathrm{is}\:\mathrm{a}\:\mathrm{cube} \\ $$$$ \\ $$$${S}\mathrm{urface}=\mathrm{2}{a}^{\mathrm{2}} +\mathrm{4}{ab}=\mathrm{216}\:\Rightarrow\:{b}=\frac{\mathrm{54}}{{a}}−\frac{{a}}{\mathrm{2}} \\ $$$${V}\mathrm{olume}={a}^{\mathrm{2}} {b}=\mathrm{54}{a}−\frac{\mathrm{1}}{\mathrm{2}}{a}^{\mathrm{3}} \\ $$$${V}'=\mathrm{54}−\frac{\mathrm{3}}{\mathrm{2}}{a}^{\mathrm{2}} =\mathrm{0}\:\Rightarrow\:{a}=\mathrm{6}\:\Rightarrow\:{b}=\mathrm{6} \\ $$
Commented by Tawa1 last updated on 02/Jun/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
