Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 59580 by maxmathsup by imad last updated on 12/May/19

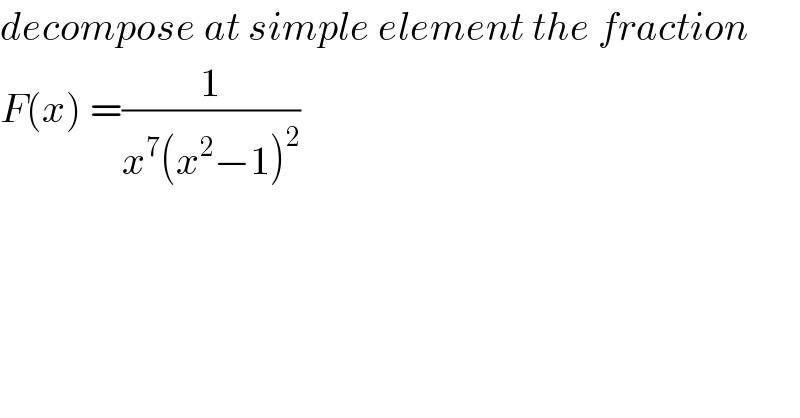
decompose at simple element the fraction F(x) =(1/(x^7 (x^2 −1)^2 ))

$${decompose}\:{at}\:{simple}\:{element}\:{the}\:{fraction}\: \\ $$$${F}\left({x}\right)\:=\frac{\mathrm{1}}{{x}^{\mathrm{7}} \left({x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$

Commented by malwaan last updated on 12/May/19

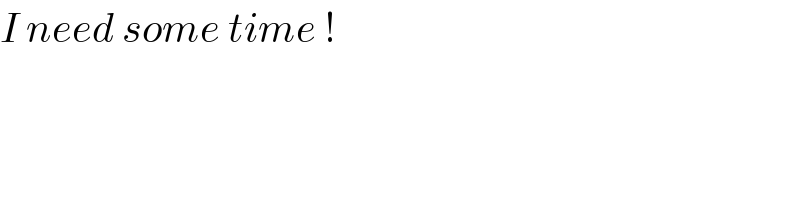
I need some time !

$${I}\:{need}\:{some}\:{time}\:! \\ $$

Answered by MJS last updated on 13/May/19

F(x)=(a/((x−1)^2 ))+(b/((x+1)^2 ))+(c/(x−1))+(d/(x+1))+(e/x)+(f/x^2 )+(g/x^3 )+(h/x^4 )+(i/x^5 )+(j/x^6 )+(k/x^7 ) the numerator of this fraction =N N−1=0 ⇒ the constant factors on the left handed side are zero: x^(10) : c+d+e=0 x^9 : a+b+c−d+f=0 x^8 : 2(a−b−e)−c−d+g=0 x^7 : a+b−c+d−2f+h=0 x^6 : e−2g+i=0 x^5 : f−2h+j=0 x^4 : g−2i+k=0 x^3 : h−2j=0 x^2 : i−2k=0 x^1 : j=0 x^0 : k−1=0 ⇒ a=(1/4); b=−(1/4); c=−2; d=−2; e=4; f=0; g=3; h=0; i=2; j=0; k=1 ⇒ F(x)=(1/(4(x−1)^2 ))−(1/(4(x+1)^2 ))−(2/(x−1))−(2/(x+1))+(4/x)+(3/x^3 )+(2/x^5 )+(1/x^7 )

$${F}\left({x}\right)=\frac{{a}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }+\frac{{b}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{{c}}{{x}−\mathrm{1}}+\frac{{d}}{{x}+\mathrm{1}}+\frac{{e}}{{x}}+\frac{{f}}{{x}^{\mathrm{2}} }+\frac{{g}}{{x}^{\mathrm{3}} }+\frac{{h}}{{x}^{\mathrm{4}} }+\frac{{i}}{{x}^{\mathrm{5}} }+\frac{{j}}{{x}^{\mathrm{6}} }+\frac{{k}}{{x}^{\mathrm{7}} } \\ $$$$\mathrm{the}\:\mathrm{numerator}\:\mathrm{of}\:\mathrm{this}\:\mathrm{fraction}\:={N} \\ $$$${N}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{constant}\:\mathrm{factors}\:\mathrm{on}\:\mathrm{the}\:\mathrm{left}\:\mathrm{handed}\:\mathrm{side} \\ $$$$\mathrm{are}\:\mathrm{zero}: \\ $$$${x}^{\mathrm{10}} :\:\:{c}+{d}+{e}=\mathrm{0} \\ $$$${x}^{\mathrm{9}} :\:\:\:\:{a}+{b}+{c}−{d}+{f}=\mathrm{0} \\ $$$${x}^{\mathrm{8}} :\:\:\:\:\mathrm{2}\left({a}−{b}−{e}\right)−{c}−{d}+{g}=\mathrm{0} \\ $$$${x}^{\mathrm{7}} :\:\:\:\:{a}+{b}−{c}+{d}−\mathrm{2}{f}+{h}=\mathrm{0} \\ $$$${x}^{\mathrm{6}} :\:\:\:\:{e}−\mathrm{2}{g}+{i}=\mathrm{0} \\ $$$${x}^{\mathrm{5}} :\:\:\:\:{f}−\mathrm{2}{h}+{j}=\mathrm{0} \\ $$$${x}^{\mathrm{4}} :\:\:\:\:{g}−\mathrm{2}{i}+{k}=\mathrm{0} \\ $$$${x}^{\mathrm{3}} :\:\:\:\:{h}−\mathrm{2}{j}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} :\:\:\:\:{i}−\mathrm{2}{k}=\mathrm{0} \\ $$$${x}^{\mathrm{1}} :\:\:\:\:{j}=\mathrm{0} \\ $$$${x}^{\mathrm{0}} :\:\:\:\:{k}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:{a}=\frac{\mathrm{1}}{\mathrm{4}};\:{b}=−\frac{\mathrm{1}}{\mathrm{4}};\:{c}=−\mathrm{2};\:{d}=−\mathrm{2};\:{e}=\mathrm{4}; \\ $$$$\:\:\:\:\:\:{f}=\mathrm{0};\:{g}=\mathrm{3};\:{h}=\mathrm{0};\:{i}=\mathrm{2};\:{j}=\mathrm{0};\:{k}=\mathrm{1} \\ $$$$\Rightarrow \\ $$$${F}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{4}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{4}\left({x}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{2}}{{x}−\mathrm{1}}−\frac{\mathrm{2}}{{x}+\mathrm{1}}+\frac{\mathrm{4}}{{x}}+\frac{\mathrm{3}}{{x}^{\mathrm{3}} }+\frac{\mathrm{2}}{{x}^{\mathrm{5}} }+\frac{\mathrm{1}}{{x}^{\mathrm{7}} } \\ $$

Commented by ajfour last updated on 12/May/19

FABULOUS Sir!

$$\mathcal{FABULOUS}\:{Sir}! \\ $$

Commented by malwaan last updated on 15/May/19

thanks sir !

$${thanks}\:{sir}\:! \\ $$

Commented by MJS last updated on 13/May/19

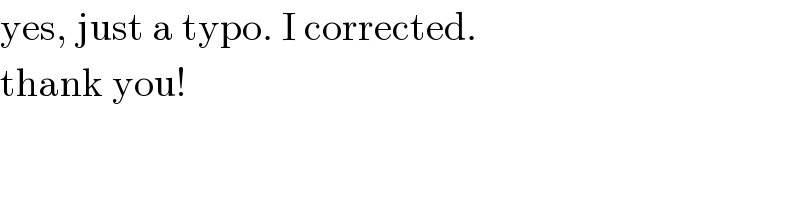
yes, just a typo. I corrected. thank you!

$$\mathrm{yes},\:\mathrm{just}\:\mathrm{a}\:\mathrm{typo}.\:\mathrm{I}\:\mathrm{corrected}. \\ $$$$\mathrm{thank}\:\mathrm{you}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com