
Question Number 5851 by sanusihammed last updated on 01/Jun/16
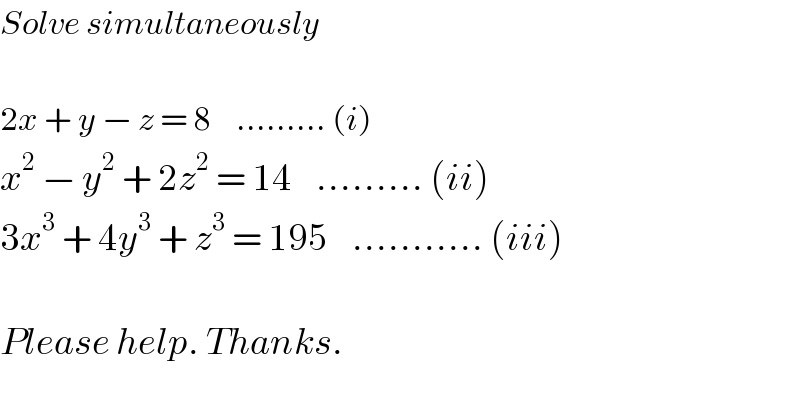
$${Solve}\:{simultaneously} \\ $$$$ \\ $$$$\mathrm{2}{x}\:+\:{y}\:−\:{z}\:=\:\mathrm{8}\:\:\:\:.........\:\left({i}\right) \\ $$$${x}^{\mathrm{2}} \:−\:{y}^{\mathrm{2}} \:+\:\mathrm{2}{z}^{\mathrm{2}} \:=\:\mathrm{14}\:\:\:\:.........\:\left({ii}\right) \\ $$$$\mathrm{3}{x}^{\mathrm{3}} \:+\:\mathrm{4}{y}^{\mathrm{3}} \:+\:{z}^{\mathrm{3}} \:=\:\mathrm{195}\:\:\:\:...........\:\left({iii}\right) \\ $$$$ \\ $$$${Please}\:{help}.\:{Thanks}. \\ $$
Commented by Yozzii last updated on 01/Jun/16

$${Suppose}\:{x},{z},{y}\in\mathbb{Z}.\:{Then}\:\mathrm{2}{x}\:{is}\:{even}. \\ $$$${Also}\:\mathrm{2}\mid\mathrm{8}\Rightarrow\:{in}\:\left({i}\right)\:\mathrm{2}\mid\left({y}−{z}\right) \\ $$$$\Rightarrow{y}\:{and}\:{z}\:{share}\:{the}\:{same}\:{parity}\:\left({even}\:{or}\:{odd}\right) \\ $$$${To}\:{see}\:{this},\:{let}\:{y}=\mathrm{2}{n},{z}=\mathrm{2}{m}\:\left({m},{n}\in\mathbb{Z}\right).\Rightarrow{y}−{z}=\mathrm{2}\left({n}−{m}\right)\:{which}\:{is}\:{even}. \\ $$$${Now}\:{let}\:{y}=\mathrm{2}{p}+\mathrm{1},{z}=\mathrm{2}{k}−\mathrm{1}\:\left({p},{k}\in\mathbb{Z}\right).\Rightarrow{y}−{z}=\mathrm{2}\left({p}−{k}+\mathrm{1}\right)\:{which}\:{is}\:{even}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Suppose}\:{in}\:{one}\:{case}\:{that}\:{y}\:{and}\:{z}\:{are} \\ $$$${odd}.\:{Then},\:\mathrm{2}{z}^{\mathrm{2}} \:{is}\:{even}\:{and}\:{y}^{\mathrm{2}} \:{is}\:{odd}. \\ $$$${But}\:{x}\in\mathbb{Z}\:{and}\:{from}\:\left({ii}\right)\:\mathrm{14}\:{is}\:{even}.\: \\ $$$${So},\:\mathrm{2}\nmid{x}^{\mathrm{2}} \:{or}\:{x}\:{is}\:{odd} \\ $$$${From}\:\left({iii}\right),\:\mathrm{195}\:{is}\:{odd},\:{z}^{\mathrm{3}} \:{is}\:{odd},\:\mathrm{4}{y}^{\mathrm{3}} \\ $$$${is}\:{even}\:{and}\:\mathrm{3}{x}^{\mathrm{3}} \:{is}\:{odd}\: \\ $$$$\Rightarrow\left({odd}\:{integer}\right)+\left({even}\:{integer}\right)+\left({odd}\:{integer}\right)=\left({odd}\:{integer}\right) \\ $$$${which}\:{is}\:{a}\:{contradiction}. \\ $$$${So},\:{y}\:{and}\:{z}\:{cannot}\:{both}\:{be}\:{odd}\:{integers}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${Suppose}\:{now}\:{that}\:{both}\:{z}\:{and}\:{y}\:{are}\:{even}. \\ $$$$\Rightarrow\:{in}\:\left({ii}\right),\:\mathrm{2}\mid{y}^{\mathrm{2}} \:{and}\:{also}\:\mathrm{2}\mid\mathrm{2}{z}^{\mathrm{2}} .\:{But}\:\mathrm{2}\mid\mathrm{14} \\ $$$${and}\:{if}\:\mathrm{2}\nmid{x}\Rightarrow\:\left({odd}\right)−\left({even}\right)+\left({even}\right)=\left({even}\right) \\ $$$${which}\:{is}\:{a}\:{contradiction}.\:{Hence},\:{x}\:{must}\:{be}\:{even}. \\ $$$${Looking}\:{at}\:\left({iii}\right),\:{since}\:\mathrm{2}\mid{x},{y},{z}\:{but}\:\mathrm{2}\nmid\mathrm{195} \\ $$$$\left({iii}\right)\:{is}\:{also}\:{contradictory}. \\ $$$$−−−−−−−−−−−−−−−−−−−−−−−−−− \\ $$$${In}\:{all},\:{no}\:{integer}\:{triple}\:\left({x},{y},{z}\right)\in\mathbb{Z}^{\mathrm{3}} \:{exists} \\ $$$${satisfying}\:{equations}\:\left({i}\right)\rightarrow\left({iii}\right)\:{concurrently}. \\ $$
Commented by sanusihammed last updated on 01/Jun/16

$${Thanks}\:.\:{i}\:{grab}= \\ $$
Commented by Rasheed Soomro last updated on 09/Jun/16
$$\mathrm{G}^{\mathcal{OO}} \mathrm{D}\:\mathrm{A}^{\mathcal{NALYSI}} \mathrm{S}\:! \\ $$
