
Question Number 57417 by Abdo msup. last updated on 03/Apr/19
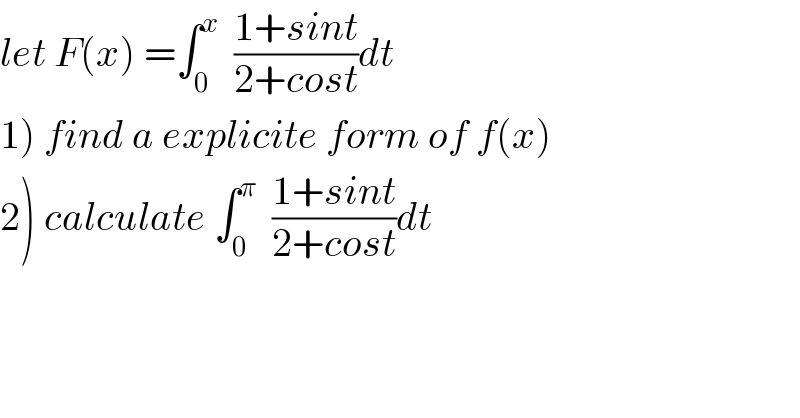
$${let}\:{F}\left({x}\right)\:=\int_{\mathrm{0}} ^{{x}} \:\:\frac{\mathrm{1}+{sint}}{\mathrm{2}+{cost}}{dt} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{explicite}\:{form}\:{of}\:{f}\left({x}\right) \\ $$$$\left.\mathrm{2}\right)\:{calculate}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{1}+{sint}}{\mathrm{2}+{cost}}{dt} \\ $$
Commented by Abdo msup. last updated on 05/Apr/19
![1)changement tan((t/2))=u give F(x)=∫_0 ^(tan((x/2))) ((1+((2u)/(1+u^2 )))/(2+((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 )) =∫_0 ^(tan((x/2))) ((1+u^2 +2u)/(2+2u^2 +1−u^2 )) ((2du)/(1+u^2 )) =2 ∫_0 ^(tan((x/2))) ((u^2 +2u +1)/((u^2 +1)(u^2 +3))) du let decompose F(u) = ((u^2 +2u +1)/((u^2 +1)(u^2 +3))) ⇒F(u) =((au +b)/(u^2 +1)) +((cu +d)/(u^2 +3)) ⇒(u^2 +3)(au+b) +(u^2 +1)(cu +d)=u^2 +2u +1 ⇒ au^3 +bu^2 +3au +3b +cu^3 +du^2 +cu +d =u^2 +2u +1 ⇒ (a+c)u^3 +(b+d)u^2 +(3a+c)u +3b +d =u^2 +2u +1⇒ a+c=0,b+d =1,3a+c =2 ,3b +d =1 ⇒ c=−a ⇒3a−a =2 ⇒a =1 wehave d=1−b ⇒ 3b +1−b =1 ⇒b=0 ⇒d=1 ⇒ F(u)=(u/(u^2 +1)) +((−u +1)/(u^2 +3)) ⇒∫ F(u)du =(1/2)ln(u^2 +1) −(1/2)ln(u^2 +3) +arctan(u) +c ⇒ F(x)=2 [(1/2)ln(u^2 +1)−(1/2)ln(u^2 +3) +arctan(u)]_0 ^(tan((x/2))) =2 {(1/2)ln(1+tan^2 ((x/2)))−(1/2)ln(3+tan^2 ((x/2)))+(x/2)} F(x)=x +ln(1+tan^2 ((x/2)))−ln(3+tan^2 ((x/2)))](Q57478.png)
$$\left.\mathrm{1}\right){changement}\:{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}\:{give} \\ $$$${F}\left({x}\right)=\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\frac{\mathrm{1}+\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}{\mathrm{2}+\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\:\:\frac{\mathrm{1}+{u}^{\mathrm{2}} \:+\mathrm{2}{u}}{\mathrm{2}+\mathrm{2}{u}^{\mathrm{2}} \:+\mathrm{1}−{u}^{\mathrm{2}} }\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\frac{{u}^{\mathrm{2}} \:+\mathrm{2}{u}\:+\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+\mathrm{3}\right)}\:{du}\:\:{let}\:{decompose} \\ $$$${F}\left({u}\right)\:=\:\frac{{u}^{\mathrm{2}} \:+\mathrm{2}{u}\:+\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+\mathrm{3}\right)}\:\Rightarrow{F}\left({u}\right)\:=\frac{{au}\:+{b}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{{cu}\:+{d}}{{u}^{\mathrm{2}} \:+\mathrm{3}} \\ $$$$\Rightarrow\left({u}^{\mathrm{2}} \:+\mathrm{3}\right)\left({au}+{b}\right)\:+\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({cu}\:+{d}\right)={u}^{\mathrm{2}} \:+\mathrm{2}{u}\:+\mathrm{1}\:\Rightarrow \\ $$$${au}^{\mathrm{3}} \:+{bu}^{\mathrm{2}} \:+\mathrm{3}{au}\:+\mathrm{3}{b}\:+{cu}^{\mathrm{3}} \:+{du}^{\mathrm{2}} \:+{cu}\:+{d}\:={u}^{\mathrm{2}} \:+\mathrm{2}{u}\:+\mathrm{1}\:\Rightarrow \\ $$$$\left({a}+{c}\right){u}^{\mathrm{3}} \:+\left({b}+{d}\right){u}^{\mathrm{2}} \:+\left(\mathrm{3}{a}+{c}\right){u}\:+\mathrm{3}{b}\:+{d}\:={u}^{\mathrm{2}} \:+\mathrm{2}{u}\:+\mathrm{1}\Rightarrow \\ $$$${a}+{c}=\mathrm{0},{b}+{d}\:=\mathrm{1},\mathrm{3}{a}+{c}\:=\mathrm{2}\:,\mathrm{3}{b}\:+{d}\:=\mathrm{1}\:\Rightarrow \\ $$$${c}=−{a}\:\Rightarrow\mathrm{3}{a}−{a}\:=\mathrm{2}\:\Rightarrow{a}\:=\mathrm{1}\:\:{wehave}\:{d}=\mathrm{1}−{b}\:\Rightarrow \\ $$$$\mathrm{3}{b}\:+\mathrm{1}−{b}\:=\mathrm{1}\:\Rightarrow{b}=\mathrm{0}\:\Rightarrow{d}=\mathrm{1}\:\Rightarrow \\ $$$${F}\left({u}\right)=\frac{{u}}{{u}^{\mathrm{2}} \:+\mathrm{1}}\:+\frac{−{u}\:+\mathrm{1}}{{u}^{\mathrm{2}} \:+\mathrm{3}}\:\Rightarrow\int\:{F}\left({u}\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\:−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({u}^{\mathrm{2}} \:+\mathrm{3}\right)\:+{arctan}\left({u}\right)\:+{c}\:\Rightarrow \\ $$$${F}\left({x}\right)=\mathrm{2}\:\left[\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({u}^{\mathrm{2}} \:+\mathrm{3}\right)\:+{arctan}\left({u}\right)\right]_{\mathrm{0}} ^{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \\ $$$$=\mathrm{2}\:\left\{\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)−\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{3}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)+\frac{{x}}{\mathrm{2}}\right\} \\ $$$${F}\left({x}\right)={x}\:+{ln}\left(\mathrm{1}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right)−{ln}\left(\mathrm{3}+{tan}^{\mathrm{2}} \left(\frac{{x}}{\mathrm{2}}\right)\right) \\ $$
Commented by Abdo msup. last updated on 05/Apr/19
![2)we have ∫_0 ^π ((1+sint)/(2+cost))dt =_(tan((x/2))) ∫_0 ^∞ ((1+((2u)/(1+u^2 )))/(2+((1−u^2 )/(1+u^2 )))) ((2du)/(1+u^2 )) =2 ∫_0 ^∞ ((u^2 +2u +1)/((u^2 +1)(u^2 +3))) du =[ln(u^2 +1)−ln(u^2 +3) +2 arctan(u)]_0 ^(+∞) =[ln(((u^2 +1)/(u^2 +3))) +2 arctan(u)]_0 ^(+∞) =π−ln((1/3)) =π +ln(3) .](Q57479.png)
$$\left.\mathrm{2}\right){we}\:{have}\:\int_{\mathrm{0}} ^{\pi} \:\:\frac{\mathrm{1}+{sint}}{\mathrm{2}+{cost}}{dt}\:=_{{tan}\left(\frac{{x}}{\mathrm{2}}\right)} \:\:\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}+\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}{\mathrm{2}+\frac{\mathrm{1}−{u}^{\mathrm{2}} }{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{u}^{\mathrm{2}} \:+\mathrm{2}{u}\:+\mathrm{1}}{\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+\mathrm{3}\right)}\:{du} \\ $$$$=\left[{ln}\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)−{ln}\left({u}^{\mathrm{2}} \:+\mathrm{3}\right)\:+\mathrm{2}\:{arctan}\left({u}\right)\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\left[{ln}\left(\frac{{u}^{\mathrm{2}} \:+\mathrm{1}}{{u}^{\mathrm{2}} \:+\mathrm{3}}\right)\:+\mathrm{2}\:{arctan}\left({u}\right)\right]_{\mathrm{0}} ^{+\infty} =\pi−{ln}\left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$$=\pi\:+{ln}\left(\mathrm{3}\right)\:. \\ $$
